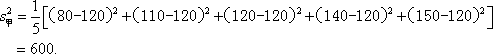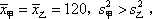- 分布的意义和作用
- 共27题
在△ABC中,角A,B,C的对边分别为a,b,c.已知3cos(B-C)-1=6cos Bcos C。
(1)求cos A;
(2)若a=3,△ABC的面积为
正确答案
(1) 

解析
(1)由3cos(B-C)-1=6cos Bcos C,
得3(cos Bcos C-sin Bsin C)=-1,
即cos(B+C)=

(2)由于0<A<π,cos A=

又S△ABC=

由余弦定理a2=b2+c2-2bccos A,得b2+c2=13.
解方程组

知识点
设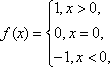

正确答案
解析
∵g(π)=0,∴f(g(π))=f(0)=0
知识点
已知随机变量ξ服从正态分布N(2,σ2),且P(ξ<4)=0.8,则P(0<ξ<2)=( )
正确答案
解析
知识点
汽车的碳排放量比较大,某地规定,从2014年开始,将对二氧化碳排放量超过130g/km的轻型汽车进行惩罚性征税,检测单位对甲、乙两品牌轻型汽车各抽取5辆进行二氧化碳排放量检测,记录如下(单位:g/km)。
经测算得乙品牌轻型汽车二氧化碳排放量的平均值为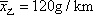
(1)从被检测的5辆甲品牌轻型汽车中任取2辆,则至少有一辆二氧化碳排放量超过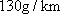
(2)求表中
正确答案
(1)0.7
(2)乙品牌轻型汽车二氧化碳排放量的稳定性好
解析
(1)从被检测的
共有
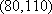
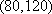
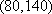
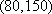
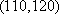
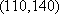
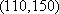
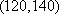
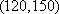
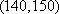
设“至少有一辆二氧化碳排放量超过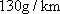
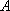
则事件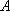
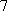
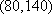
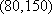
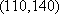
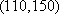
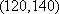
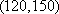
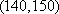
所以 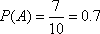
即至少有一辆二氧化碳排放量超过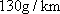
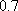
(2)由题可知,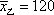
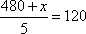
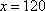
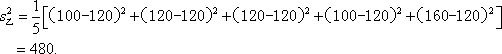
因为
所以乙品牌轻型汽车二氧化碳排放量的稳定性好, ………………13分
知识点
在如下数表中,已知每行、每列中的树都成等差数列,
那么,位于下表中的第n行第n+1列的数是 。
正确答案
解析
第n行第一列的数为n,观察得,第n行的公差为n,所以第n0行的通项公式为


知识点
经销商经销某种农产品,在一个销售季度内,每售出1 t该产品获利润500元,未售出的产品,每1 t亏损300元,根据历史资料,得到销售季度内市场需求量的频率分布直方图,如图所示,经销商为下一个销售季度购进了130 t该农产品,以X(单位:t,100≤X≤150)表示下一个销售季度内的市场需求量,T(单位:元)表示下一个销售季度内经销该农产品的利润。
(1)将T表示为X的函数;
(2)根据直方图估计利润T不少于57 000元的概率。
正确答案
(1)
(2)0.7.
解析
(1)当X∈[100,130)时,T=500X-300(130-X)=800X-39 000.
当X∈[130,150]时,T=500×130=65 000.
所以
(2)由(1)知利润T不少于57 000元当且仅当120≤X≤150.
由直方图知需求量X∈[120,150]的频率为0.7,所以下一个销售季度内的利润T不少于57 000元的概率的估计值为0.7.
知识点
已知




正确答案
解析
略。
知识点
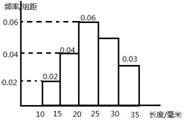
对一批产品的长度(单位: mm)进行抽样检测, 下图喂检测结果的频率分布直方图. 根据标准, 产品长度在区间[20,25)上的为一等品, 在区间[15,20)和区间[25,30)上的为二等品, 在区间[10,15)和[30,35)上的为三等品. 用频率估计概率, 现从该批产品中随机抽取一件, 则其为二等品的概率为()
正确答案
解析
组距为5,二等品的概率为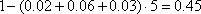
知识点
在“世界读书日”前夕,为了了解某地5 000名居民某天的阅读时间,从中抽取了200名居民的阅读时间进行统计分析,在这个问题中,5 000名居民的阅读时间的全体是( )
正确答案
解析
由题意知,5 000名居民的阅读时间是总体,200名居民的阅读时间为一个样本;每个居民的阅读时间为个体;200为样本容量;故选A.
知识点
某工厂有25周岁以上(含25周岁)工人300名,25周岁以下工人200名,为研究工人的日平均生产量是否与年龄有关,现采用分层抽样的方法,从中抽取了100名工人,先统计了他们某月的日平均生产件数,然后按工人年龄在“25周岁以上(含25周岁)”和“25周岁以下”分为两组,在将两组工人的日平均生产件数分成5组:




(1)从样本中日平均生产件数不足60件的工人中随机抽取2人,求至少抽到一名“25周岁以下组”工人的频率。
(2)规定日平均生产件数不少于80件者为“生产能手”,请你根据已知条件完成

附表:
正确答案
见解析
解析
本小题主要考查古典概型、抽样方法、独立性检验等基础知识,考查运算求解能力、应用意识,考查必然和或然思想、化归与转化思想等,满分12分。
(1)由已知得,样本中有



所以,样本中日平均生产件数不足


记为





从中随机抽取










其中,至少有名“








(2)由频率分布直方图可知,在抽取的





所以得:
因为

知识点
扫码查看完整答案与解析