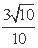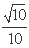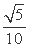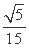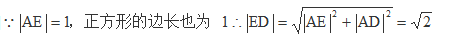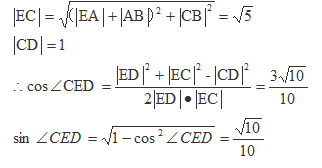- 几何证明选讲
- 共124题
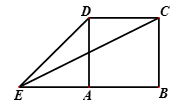
如图,


(1)AC·BD=AD·AB;
(2)AC=AE。
正确答案
见解析
解析
证明:(1)由AC与
同理∠ACB=∠DAB,
所以△ACB∽△DAB。
从而
(2)由AD与
又∠ADE=∠BDA,得△EAD∽△ABD。
从而
结合(1)的结论,AC=AE
知识点
如图,正方形
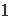
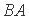
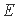
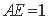
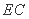
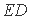
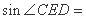
正确答案
解析
知识点
如图3,










两点,已知


正确答案
解析
略
知识点
在△









正确答案
解析
略
知识点
如图,半径为2的⊙O中,





正确答案
解析
略
知识点
如图,已知△ABC内接于⊙O,点D在OC的延长线上,AD切⊙O于A,若∠ABC=30°,AC=2,则AD的长为 。
正确答案
解析
∵OA=OC,∠AOC=60°,
∴△AOC是等边三角形,
∴OA=AC=2,
∵∠OAD=90°,∠D=30°,
∴AD=

故答案为:
知识点
如图3,在





正确答案
10
解析
略
知识点
如图所示,





正确答案
解析
连结



且


知识点
从下列题中选答1题。
22.(几何证明选讲)
如图,AD是⊙O的直径,AB是⊙O的切线,M, N是圆上两点,直线MN交AD的延长线于点C,交⊙O的切线于B,BM=MN=NC=1,求AB的长和⊙O的半径.
23.(极坐标和参数方程)
以直角坐标系原点O为极点,x轴正半轴为极轴,并在两种坐标系中取相同的长度单位.已知直线l的参数方程为

(Ⅰ)求曲线C的直角坐标方程;
(Ⅱ)设直线l与曲线C相交于A、B两点,当α变化时,求|AB|的最小值.
24.(不等式选讲)
设函数





正确答案
22.
23.
24.
解析
解析已在路上飞奔,马上就到!
知识点
22.选修4一l:几何证明选讲
如图,已知AP是圆O的切线,P为切点,AC是圆O的割线,与圆O交于B,C两点,圆心O在
(Ⅰ)证明A,P,O,M四点共圆;
(Ⅱ)求
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析