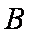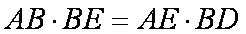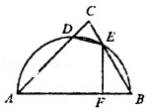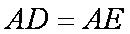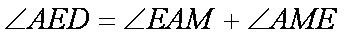- 几何证明选讲
- 共124题
如图,圆










正确答案
8
解析
略
知识点
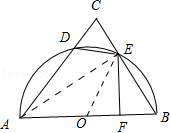
如图4所示,AB与⊙O切于点B,AO交⊙O于点C、D,且AO=5,AB=4,则⊙O的半径长=_____.则△ABD的面积是___________.
正确答案
解析
解法一:
过点B作AD的垂线,垂足为E,由AO=5,AB=4得OB=OD=3。
由
解法二:过点D作DE⊥AE于E,由
知识点
如图4,过点P的直线与圆O相交于A,B两点,若PA=1,AB=2,PO=3,则圆O的半径等于_____________________.
正确答案
解析
知识点
如图,



则
正确答案
解析
略
知识点
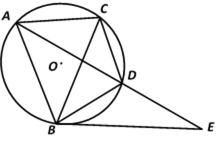
如图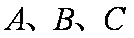
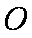
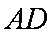
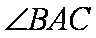
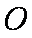
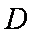
作圆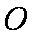
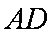
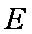
(1)求证: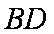
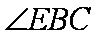
(2)求证: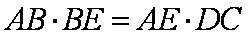
正确答案
见解析
解析
证明:(1)∵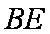

而
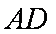
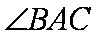
∴ 
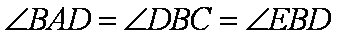
∴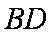

(2)由(1)可证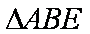
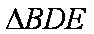
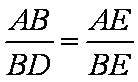
又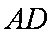
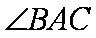
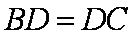
∴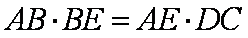
知识点
如图,以△ABC的边AB为直径的半圆交AC于点D,交BC于点E,EF⊥AB于点F,AF=3BF,BE=2EC=2.那么CD=
正确答案
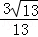
解析
解:如图所示,设圆心为点O,半径为R,连接OE,AE。
由AB为⊙O的直径,∴∠AEB=90°,∴AE⊥CE。
∵AF=3FB,AF+FB=2R,
∴FB=
∴∠ABE=60°。
∴AE=BEtan60°=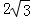
在Rt△ACE,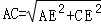
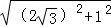
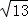
由割线定理可得:CD•CA=CE•CB,∴
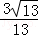
故答案为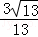
知识点
如图,点A、B、C都在⊙O上,过点C的切线交AB的延长线于点D,若AB=5,BC=3,CD=6,则线段AC的长为 。
正确答案
4.5
解析
∵过点C的切线交AB的延长线于点D,
∴DC是圆的切线,DBA是圆的割线,
根据切割线定理得到DC2=DB•DA,
∵AB=5,CD=6,
∴36=DB(DB+5)
∴DB=4,
由题意知∠D=∠D,∠BCD=∠A
∴△DBC∽△DCA,
∴
∴AC=
知识点
如图,已知⊙O中,直径AB垂直于弦CD,垂足为M,P是CD延长线上一点,PE切⊙O于点E,连接BE交CD于点F,证明:
(1)∠BFM=∠PEF;
(2)PF2=PD·PC.
正确答案
见解析
解析
(1)连接OE,
∵PE切⊙O于点E,∴OE⊥PE.
∴∠PEF+∠FEO=90°。
又∵AB⊥CD,
∴∠B+∠BFM=90°。
又∵∠B=∠FEO,
∴∠BFM=∠PEF.
(2)∵∠EFP=∠BFM,
∴∠EFP=∠PEF.
∴PE=PF.
又∵PE2=PD·PC,
∴PF2=PD·PC.
知识点
已知AB为圆O的直径,AB=4,C为半圆上一点,过点C作圆O的切线CD,过点A作AD
正确答案
2
解析
试题分析:
连结








过点












知识点
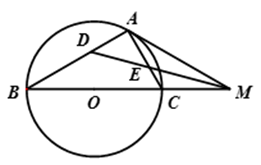
已知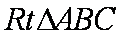
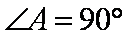
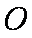
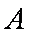
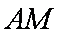
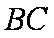
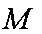
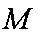
交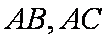
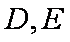
(1)求证: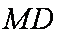
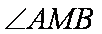
(2)若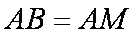
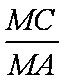

正确答案
见解析
解析
证明:(1)由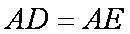

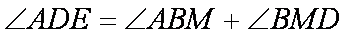
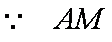
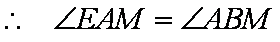

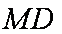
(2)由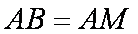
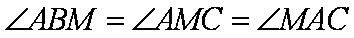
即
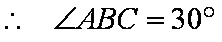
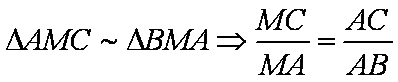
知识点
扫码查看完整答案与解析