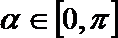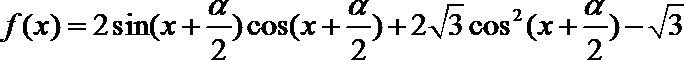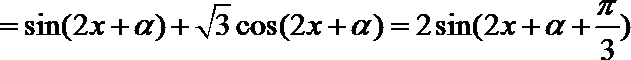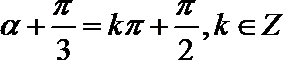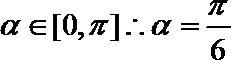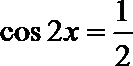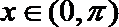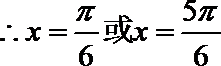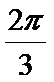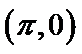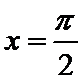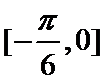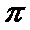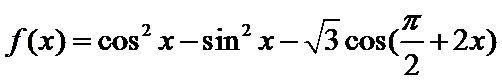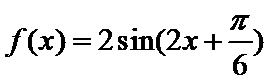- 三角函数与三角恒等变换
- 共3475题
6.把函数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9. 
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16. 已知函数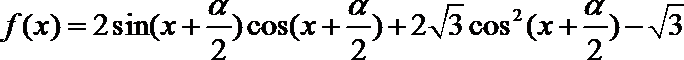
(Ⅰ)求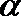
(Ⅱ)若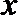

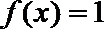
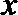
正确答案
解:(Ⅰ)
由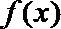
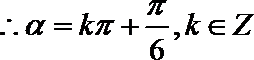
(Ⅱ)由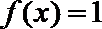
又 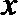
解析
解析已在路上飞奔,马上就到!
知识点
15.若函数

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
23. 下列说法正确的是( )(填上你认为正确的所有命题的序号)
①函数
②函数

③函数

④


⑤函数
正确答案
①③④⑤
解析
解析已在路上飞奔,马上就到!
知识点
2.函数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7. 函数



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.在△ABC中三边之比a:b:c=2:3: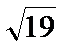
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8. 设



① 
② 既不是奇函数也不是偶函数;
③ 

④ 存在经过点

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.函数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.已知函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.设函数









正确答案
解析
在
若
则

∴

∴
∴
故选C.
考查方向
本题考查函数的性质,考查即时学习能力,是中档题.新定义的学习型问题,在近几年各省市高考中出现的频率很高,常以压轴题的形式出现,整合函数、数列、解析几何、三角、向量等知识,体现数学多种思想方法.
解题思路
先求


易错点
对新定义对称中心的不理解.
知识点
7.定义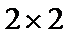
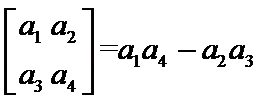
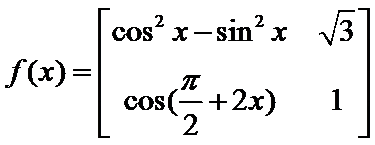
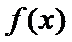
正确答案
解析
根据矩阵的定义,可以得到
所以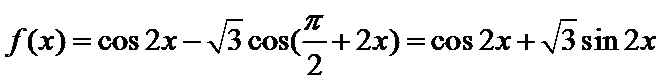
根据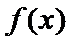
考查方向
三角函数
解题思路
先根据矩阵的定义,得到f(x)的解析式,然后根据函数的解析式判断函数的相关性质.
易错点
三角函数公式记忆混淆
知识点
已知





正确答案
解析
由







考查方向
本题主要考查了矩阵的概念,三角函数图像与性质的综合应用
易错点
函数平移的对象是x,这是解决函数平移的问题的关键
知识点
扫码查看完整答案与解析