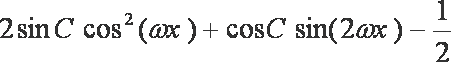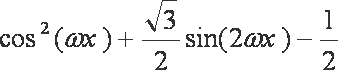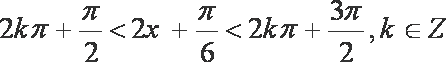- 三角函数与三角恒等变换
- 共3475题
在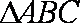

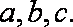
(1)求角A的大小;(2)若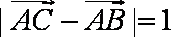
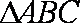
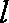
正确答案
(1)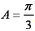
解析
解析:(1)在△ABC中,∵
由正弦定理有: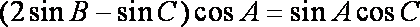
∴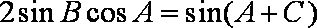
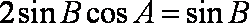
∵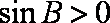
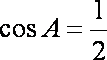
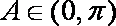

(2)由已知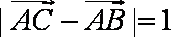
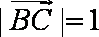
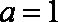
由正弦定理得: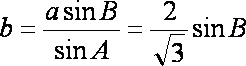
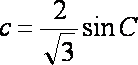
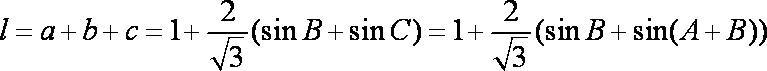
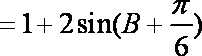
∵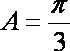
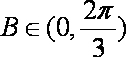
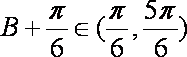
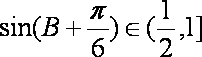
故△ABC的周长l的取值范围是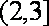
解法二:周长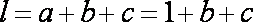
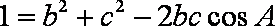
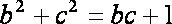
∴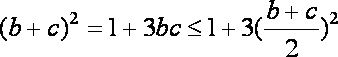
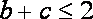
又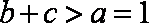
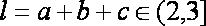
即△ABC的周长l的取值范围是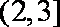
知识点
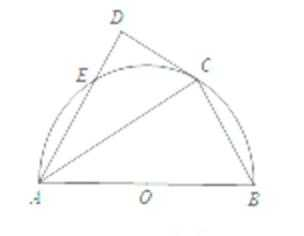
已知△ABC中,D是BC边的中点,过点D的直线分别交直线AB、AC于点E、F,若

正确答案
解析
由已知得:

所以

因为D,E,F三点共线,
所以
又
所以

故选:A
知识点
已知

(1)若

(2)若函数y=f(x)的定义域为[
正确答案
(1)
解析
(1)f(x)=-2asin2x+2asinxcosx+a+b=2asin+b,
∵a>0,∴由2kπ-≤2x+≤2kπ+得, kπ-≤x≤kπ+,k∈Z。
∴函数y=f(x)的单调递增区间是[kπ-,kπ+](k∈Z)
(2)x∈[,π]时,2x+∈[,], sin∈[-1,]
当a>0时,f(x)∈[-2a+b,a+b]
当a<0时,f(x)∈[a+b,-2a+b]
综上知,
知识点
已知椭圆



(1) 求椭圆的方程;
(2) 设垂直于



(3) 过点




正确答案
见解析
解析
解:(1)由


(2)设

又

当且仅当
从而

(3)因为A(-1,0),所以
由


∴点
同理,有

∴

即
所以

知识点
已知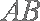

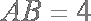


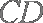
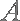
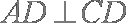

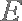
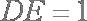
(1)求证: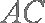
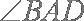
(2)求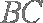
正确答案
见解析
解析
(1)连结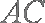
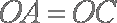
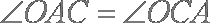
因为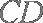
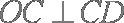
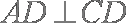
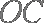
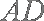
所以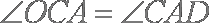
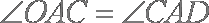
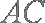
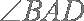
(2)由(1)知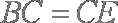
连结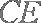
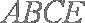

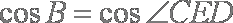
所以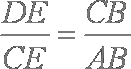
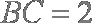
知识点
设函数



(1)求
(2)在








正确答案
见解析
解析
(1)

令

(2)由


∵
又∵

∴在

由

知识点
已知函数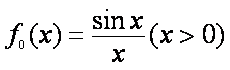
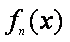
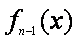
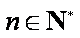
(1)求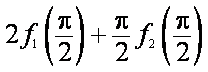
(2)证明:对任意的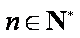
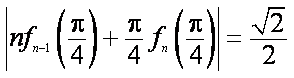
正确答案
见解析。
解析
(1)由已知,得
于是
所以
故
(2)证明:由已知,得
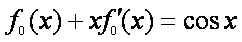
即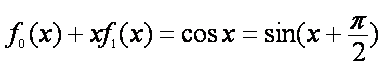
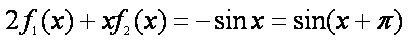
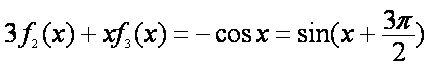
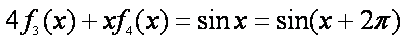
下面用数学归纳法证明等式
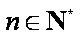
(i)当n=1时,由上可知等式成立.
(ii)假设当n=k时等式成立, 即
因为
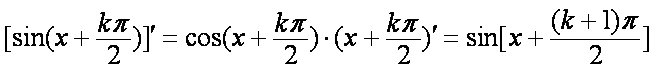
所以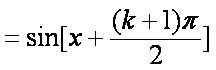
所以当n=k+1时,等式也成立.
综合(i),(ii)可知等式
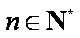
令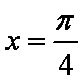
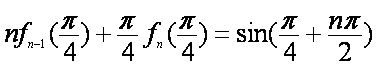
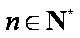
所以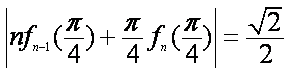
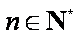
知识点
在




(1)若

(2)若

正确答案
(1)
解析
解析:(1)由正弦定理


由于


所以
(2)依题意,


又

另解:
由于


由于

由

由勾股定理

知识点
设函数



(1)求
(2)在








正确答案
见解析
解析
(1)

令

(2)由


∵
又∵

∴在

由

知识点
已知二项式
正确答案
8
解析
依题意有T3=Cn(2)(x(3))n-2(-x(1))2=2(n(n-1))x3(n-8)中x的指数为0,所以n=8.
知识点
已知在



(1)求角A、B、C的大小;
(2)设函数

正确答案
(1)

解析
解析:(1)由题设及正弦定理知:
∴


当




当


∴

(2) 由(1)及题设知:
当

即

它的相邻两对称轴间的距离为 
知识点
在△ABC中,a,b,c是角A,B,C对应的边,向量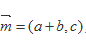
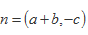
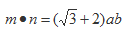
(1)求角C;
(2)函数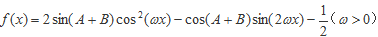
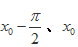
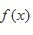
正确答案
见解析
解析
解析:(1)因为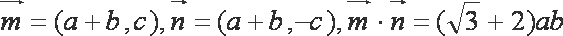
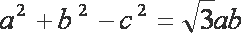
故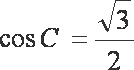
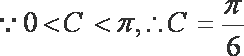
(2)
=
=
=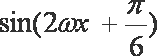
因为相邻两个极值的横坐标分别为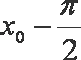
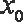
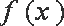
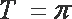
所以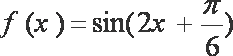
由
所以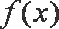
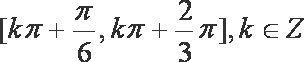
知识点
在





(1)求角
(2)当

正确答案
见解析
解析
(1)由

由正弦定理得



(2)

由

即


知识点
如图,在四棱锥P—ABCD中,PA⊥AD,AB∥CD,CD⊥AD,AD = CD = 2AB = 2,E,F分别为PC,CD的中点,DE = EC。
(1)求证:平面ABE⊥平面BEF;
(2)设PA = a,若平面EBD与平面ABCD所成锐二面角
正确答案
见解析
解析
(1)












(2) 

又



法一:建系







平面





法二:连






则



作



连


在

解得
知识点
设函数


(1)求

(2)求函数
正确答案
见解析
解析
(1)







又



当且仅当



(2)由

得





知识点
扫码查看完整答案与解析