- 三角函数与三角恒等变换
- 共3475题
5.若
正确答案
知识点
19. 关于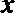
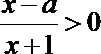
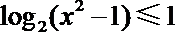
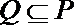
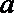
正确答案
当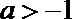
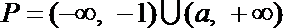
当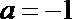
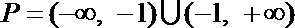
当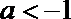
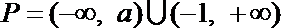
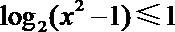
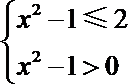
所以
所以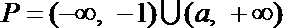
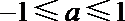
解析
解析已在路上飞奔,马上就到!
知识点
14.已知奇函数




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3. 如图,B地在A地的正东方向4 km处,C地在B地的北偏东30°方向2 km处,河流的沿岸PQ(曲线)上任意一点到A的距离比到B的距离远2 km.现要在曲线PQ上选一处M建一座码头,向B、C两地转运货物.经测算,从M到B、M到C修建公路的费用都是a万元/km,那么修建这两条公路的总费用最低是 ( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.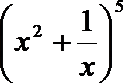
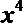
正确答案
10
解析
解析已在路上飞奔,马上就到!
知识点
13. 函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21.【选做题】
在A、B、C、D四小题中只能选做两小题。解答时应写出文字说明、证明过程或演算步骤。
A.几何证明选讲
如图,从圆O外一点P作圆O的两条切线,切点分别为A,B,AB与OP交于点M,设CD为过点M且不过圆O的一条弦,求证:O、C、P、D四点共圆。
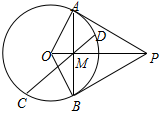
B.矩阵与变换
设矩阵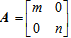
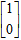
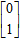
C.极坐标与参数方程
在极坐标系中,已知点O(0,0),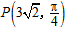
D.不等式选讲
设正实数a,b满足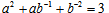
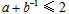
正确答案
A.
B.
C.
D.
解析
解析已在路上飞奔,马上就到!
知识点
6.若

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.直线
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.由一条曲线




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.在锐角三角形


正确答案
8;
解析
由

可得
由三角形

在(*)式两侧同时除以

又
则
由

令


由(#)得






当且仅当


解得


考查方向
解题思路
根据诱导公式、和差角公式化简,利用两边同除得到正切关系,应用正切公式的变形分析表示出
易错点
公式变形,函数关系转化,函数思想应用。
知识点
如图,
















20. 求

21. 已知警员的对讲机的有效通话距离是





正确答案
(1)

解析
试题分析: (1)由题意可得

(1)
记乙到


在

所以
考查方向
解题思路
解三角形时,有时可用正弦定理,有时也可用余弦定理,应注意用哪一个定理更方便、简捷.如果式子中含有角的余弦或边的二次式,要考虑用余弦定理;如果遇到的式子中含有角的正弦或边的一次式时,则考虑用正弦定理;以上特征都不明显时,则要考虑两个定理都有可能用到.
易错点
实际问题数学模型的转化
正确答案
(2)

解析
试题分析:(2) 分段求出对应函数解析式,根据函数单调性求得最值即可.
(2)甲到达






当

当

所以
因为








考查方向
解题思路
分段求出各个段上的函数解析式及定义域.
易错点
分段函数单调性最值的求解
在

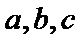
16.证明:
17.若

正确答案
由正弦定理得
故
于是
又




因此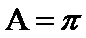

所以,
解析
见答案
考查方向
解题思路
先利用三角形正弦定理进行边角互化,再将角C用A,B表示,化简即可以得到结论
易错点
两正弦相等可能会缺少两角互补的情况
正确答案

解析
由
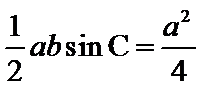

因




当



综上,

考查方向
解题思路
选择恰当的面积公式,进行边角互化。
易错点
两正弦相等可能会缺少两角互补的情况
3.在△ABC中,若

正确答案
解析
设
由余弦定理得:



考查方向
解题思路
利用正、余弦定理解三角形其关键是运用两个定理实现边角互化,从而达到知三求三的目的.本题直接根据余弦定理进行计算即可。
易错点
对余弦定理不熟悉导致出错。
知识点
13.已知三棱镜的四个面都是腰长为2的等腰三角形,该三棱锥的正视图如图所示,则该三棱锥的体积是 。
正确答案
解析
由题可知,∵三棱锥每个面都是腰为2的等腰三角形,由正视图可得如下俯视图,且三棱锥高为
考查方向
解题思路
本题考查三视图,考查几何体体积,考查学生的识图能力.解题时要求我们根据三视图想象出几何体的形状,由三视图得出几何体的尺寸,为此我们必须掌握基本几何体(柱、锥、台、球)的三视图以及各种组合体的三视图.
易错点
本题考查三视图,考查几何体体积,考查学生的识图能力.在识图时易错。
知识点
扫码查看完整答案与解析