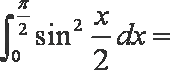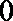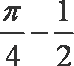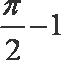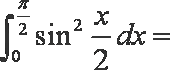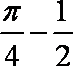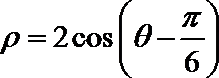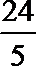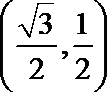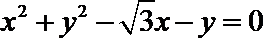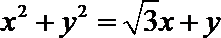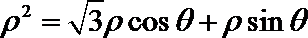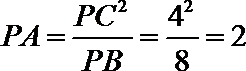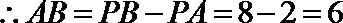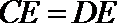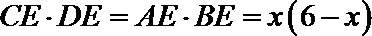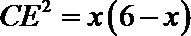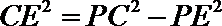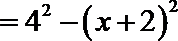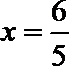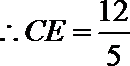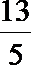- 三角函数与三角恒等变换
- 共3475题
5.
正确答案
解析
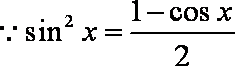
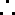
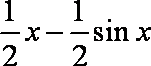
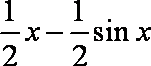
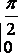
知识点
6.若



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.已知
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2. 已知

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15. 在△ABC中,a、





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1.
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
选做题: 第14、15题为选做题, 两题全答的, 只计前一题的得分。
14.以极坐标系中的点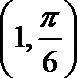
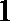
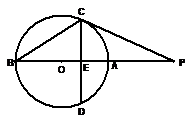
15.如图,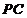
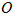
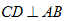
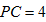
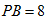
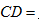
正确答案
14. 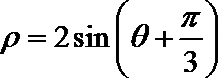
15.
解析
14.
极坐标系中的点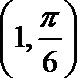
故在以极坐标系中的点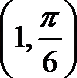
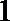
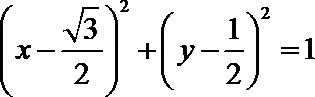
即
化为极坐标方程得
化简得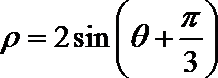
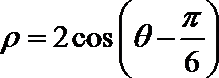
15.
由于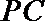
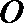
由切割线定理得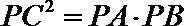
由于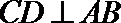
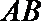
由垂径定理知
设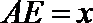
即
由勾股定理得
故有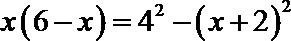
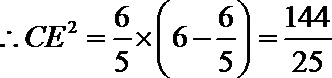
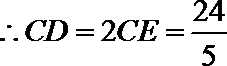
知识点
11.


正确答案
2
解析
解析已在路上飞奔,马上就到!
知识点
15. 已知

(1)求
(2)求
正确答案
(1)
所以
所以
(2)

因为

所以
又

所以
解析
解析已在路上飞奔,马上就到!
知识点
9.在




正确答案
解析
设
即
由于


知识点
17.在



(I)求角
(II)求

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.设


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.如图所示,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=2,AB=1,BM⊥PD于点M。
(1)求证:AM⊥PD;
(2)求直线CD与平面ACM所成的角的余弦值。
正确答案
(1)证明:∵PA⊥平面ABCD,
AB⊂平面ABCD,∴PA⊥AB.
∵AB⊥AD,AD∩PA=A,AD⊂平面PAD,
PA⊂平面PAD,∴AB⊥平面PAD.
∵PD⊂平面PAD,∴AB⊥PD,
∵BM⊥PD,AB∩BM=B,AB⊂平面ABM,
BM⊂平面ABM,∴PD⊥平面ABM.
∵AM⊂平面ABM,∴AM⊥PD.
解析
解析已在路上飞奔,马上就到!
知识点
5.曲线
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.在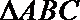
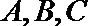
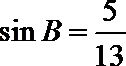
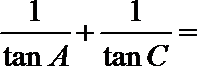
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析