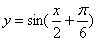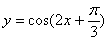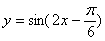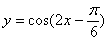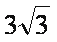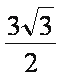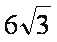- 三角函数与三角恒等变换
- 共3475题
下列函数是偶函数,且在
正确答案
解析
略
知识点
如图(4),AB是半圆的直径,C是AB延长线上一点,CD切半圆于点D,CD=2,DE⊥AB,垂足为E,且E是OB的中点,则BC的长为 。
正确答案
解析



知识点
在四棱锥






(1)求证:

(2)求证:

(3)求二面角
正确答案
见解析
解析
(1)证明:设

∵


∴


∵


∴

(2)∵

∵

又∵


∴
∵



∴

(3)以




………………8分
∵



设




∴同理可证





设平面

∴

∴
∴
∴二面角

知识点


正确答案
解析
略
知识点
同时具有性质“①最小正周期是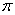
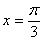
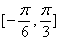
正确答案
解析
略
知识点
在三角形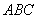
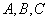
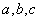
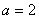
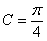
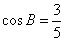
(1)求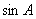
(2)求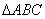
正确答案
(1)
(2)
解析
(1)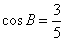
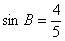
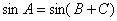
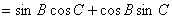
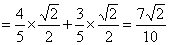
(2)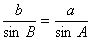
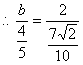
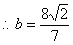
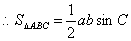
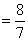
知识点
已知


正确答案
解析
略
知识点
已知函数
(1)求函数
(2)若

正确答案
见解析。
解析
(1)由

所以函数

(2)解法1:由


∴
解法2:由

代入




∴
知识点
已知函数
(1)求函数
(2)若

正确答案
见解析。
解析
知识点
已知

(1)求证:
(2)若

正确答案
见解析。
解析
(1)证明:如图
即有
(2)由
由



故
知识点
椭圆




正确答案
解析
因为椭圆的离心率为










知识点
在



(1)求角B的取值范围;
(2)若关于B的不等式
正确答案
(1)
解析
解析:(1)
当且仅当


(2)
=

故原不等式恒成立,即


知识点
如下图,某几何体的正视图与侧视图都是边长为1的正方形,且体积是
正确答案
解析
若俯视图为A,则几何体为边长为1的正方体,所以体积为1,不满足条件;若为B,则该几何体为底面直径为1,高为1的圆柱,此时体积为



知识点
一个底面为正三角形且侧棱垂直于底面的三棱柱内接于半径为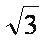
正确答案
解析
设该三棱柱的底面边长为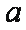
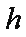
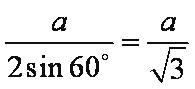
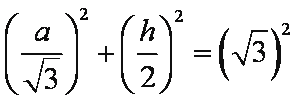
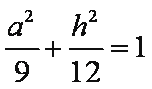
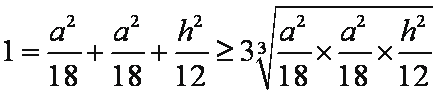
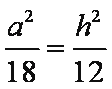
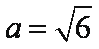
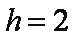
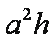
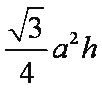
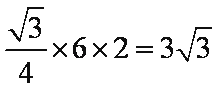
知识点
已知
正确答案
-
解析
∵cos(




∴cosα=1﹣2sin2

cos2α=2cos2α ﹣1=2×(
知识点
扫码查看完整答案与解析