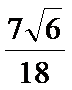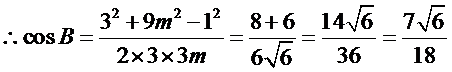- 三角函数与三角恒等变换
- 共3475题
△ABC中,
17.求BC的长;
18.求△DBC的面积。
正确答案
3
解析
解∵cos∠ABC
在△ABC中,设BC=a,AC=3b ∴9b2=
在△ABD中, cos∠ADB=
在△BDC中, cos∠BDC=
cos∠ADB=-cos∠BDC


由①②
考查方向
解题思路
利用角的关系,利用余弦定理得到边的关系,通过解方程求得BC长。
易错点
含有a的方程不易处理。
正确答案
解析
解

考查方向
解题思路
利用角的关系,利用余弦定理得到边的关系,通过解方程求得BC长。
易错点
含有a的方程不易处理。
5. 在




正确答案
解析
由正弦定理得



考查方向
解题思路
1.先利用正弦定理求出角C;2.利用大边对大角求出角C的准确值。
易错点
1.不知道应该用什么定理;2.不会根据大边对大角舍去一个角,导致结果出错。
知识点
如图,在平面四边形





17.求
18.求
正确答案
(1) 
解析
(Ⅰ)在

即


由正
考查方向
解题思路
先利用余弦定理求出
易错点
不知道该在哪个三角形中使用什么定理;
正确答案
;(2)
解析
(Ⅱ)由(Ⅰ)有:

所以
由正弦定理得:
考查方向
解题思路
利用第(1)问的结论求出
易错点
意识不到
如图所示,在四边形





16.求△
17.若

正确答案
见解析
解析
(Ⅰ)
因为

所以△ACD的面积
考查方向
解题思路
利用已知条件求出∠D角的正弦函数值,然后求
易错点
主要易错于计算出错,
正确答案
见解析
解析
(Ⅱ)在△ACD中,
所以
在△ABC中,
把已知条件代入并化简得:

考查方向
解题思路
利用余弦定理求出AC,通过
易错点
主要易错于计算出错,
16.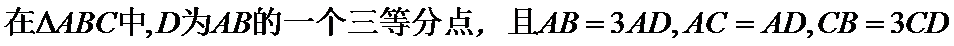
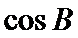
正确答案
解析
令AC=AD=1,CD=x > 0 , 则 AB=3 , BC= 3x ,
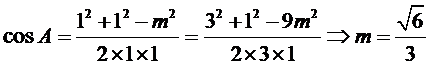
考查方向
解题思路
1.先设出题中需要的线段的长度;
2.根据余弦定理求出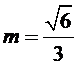
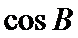
易错点
1.不会设出长度解决问题;
2.不会利用角A的余弦构造方程解方程。
知识点
在△ABC中,已知AB=2,AC=3,A=60°.
17.求BC的长;
18.求sin2C的值.
正确答案
解析
(1)由余弦定理可得:BC2=AB2+AC2﹣2AB•ACcosA=4+8﹣2×2×3×
所以BC=
考查方向
解题思路
直接利用余弦定理求解即可。
易错点
本题考查余弦定理的应用,正弦定理的应用,在计算时易错。
正确答案
解析
由正弦定理可得:



∵AB<BC,∴C为锐角,
则cosC=


因此sin2C=2sinCcosC=2×

考查方向
解题思路
利用正弦定理求出C的正弦函数值,然后利用二倍角公式求解即可.
易错点
本题考查二倍角的三角函数,在限制角的范围过程中易错。
乙是A市的建材经销商,因资金周转困难,便从A市甲处借了50万元人民币,购买了一批建材,并销售给了B市的丙,约定价款为60万元人民币,但丙未付款。乙与丙约定的合同履行地在A市。后来,甲要求乙还钱,乙说因为丙没有支付货款,所以无力偿还。鉴于此,甲欲直接起诉丙,要求其支付50万元。如果甲对丙提起诉讼,法院在下列何种情形下应当受理( )。
A.甲对乙的债权未到期
B.甲向A市的法院起诉
C.乙不愿意通过诉讼或仲裁的方式主张对丙的到期债权
D.甲以乙的名义起诉
正确答案
C
解析
暂无解析
15.在
(1)求BC的长;
(2)求
正确答案
(1)由余弦定理知,
所以
(2)由正弦定理知,

因为


因此
解析
解析已在路上飞奔,马上就到!
知识点
17.








(1)求
(2)若


正确答案
(1)因为

由正弦定理,得
又

由于
(2)解法一:由余弦定理,得
而
得
因为

故

解法二:又正弦定理,得
从而
又由


故
所以

解析
解析已在路上飞奔,马上就到!
知识点
解答题:解答应写出文字说明、证明过程或演算步骤。
17.(本题满分12分)







(Ⅰ) 求
(Ⅱ)若



正确答案
(Ⅰ)


(Ⅱ)因为








解析
解析已在路上飞奔,马上就到!
知识点
正确答案
知识点
已知函数
17.求函数
18.在




正确答案
解析
(1)由图象知A=1, 
将点


所以
考查方向
解题思路
利用函数的图象,求出A,通过函数的周期求出ω,通过函数的图象经过


易错点
三角函数的解析式中,求的值是难点,熟悉正余弦函数图象是关键.
正确答案
解析
由
所以
因为

所以

所以
考查方向
解题思路
利用

易错点
无
已知函数
17.求函数
18.在




正确答案
解析
(1)由图象知A=1, 
将点


所以
考查方向
解题思路
利用函数的图象,求出A,通过函数的周期求出ω,通过函数的图象经过


易错点
三角函数的解析式中,求的值是难点,熟悉正余弦函数图象是关键.
正确答案
解析
由
所以
因为

所以

所以
考查方向
解题思路
利用

易错点
无
正确答案
LUE
知识点
正确答案
略
知识点
扫码查看完整答案与解析