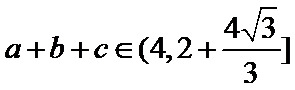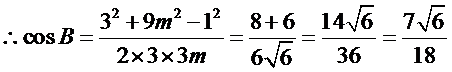- 三角函数与三角恒等变换
- 共3475题
11.如图,在




正确答案
解析






考查方向
解题思路
平面向量的数量积计算问题,往往有两种形式,一种是数量积的定义,而是利用数量积的坐标运算公式,涉及几何图形的问题,可利用几何性质用一组已知基底数量积表示所求数量积。
易错点
1、本题易直接使用数量积的定义,而不知如何计算夹角。
2、不会选择一组基底,从而用向量的加减运算及利用几何性质用一组已知基底数量积表示所求数量积
知识点
16.已知向量
(I)求函数
(II)在




正确答案
(1)


(2)
解析
试题分析:本题属于三角函数中的基本问题,题目的难度是逐渐由易到难,直接按照步骤来求
(Ⅰ)
=
由
所以函数的单调递增区间为[
(Ⅱ)
由
考查方向
解题思路
本题考查三角函数与解三角形,解题步骤如下:
1、利用向量的数量积求出
2、利用余弦定理求出
易错点
第一问中的辅助角容易计算错误
知识点
在△



17.若

18.若

正确答案

解析
试题分析:本题属于正余弦定理的综合应用问题,属于简单题,只要掌握相关的知识,即可解决本题,解析如下:
因为



因为


因此
考查方向
解题思路
直接利用正弦定理及边角关系进行计算;
易错点
相关知识点不熟容易处错。
正确答案

解析
试题分析:本题属于正余弦定理的综合应用问题,属于简单题,只要掌握相关的知识,即可解决本题,解析如下:
设



考查方向
解题思路
设


易错点
相关知识点不熟容易处错。
13.锐角三角形ABC中,


正确答案
解析
利用正弦定理得出
又∵
考查方向
解题思路
该题解题思路如下1、利用正弦定理得出


易错点
该题易于忽略了对A的范围的判断,该题属于中档题
知识点
已知



17.求
18.若

正确答案

解析
∵

∴




考查方向
解题思路
第一问中用两角和差公式和三角恒等变换化简得到

易错点
第一问中想不到将角

正确答案

解析
∵




∴


考查方向
解题思路
第二问中用倍余弦定理得到一个角,在用三角形面积公式求得面积。
易错点
第二问中用余弦定理求角时容易将特殊角记错。
在△ABC中,角A、B、C所对的边分别为a、b、c,且满足cos2C-cos2A=2sin(

17.求角A的值;
18.若a=
正确答案
见解析
解析
(1)由已知得
化简得


考查方向
解题思路
该题解题思路如下
1)利用倍角公式
2)利用特殊角的三角函数求值得到角A,
3)使用正弦定理,进行边角之间的转换
4)根据角的取值范围得到答案
易错点
该题易于忽略了对A的范围的判断,该题属于中档题
正确答案
见解析
解析
解:
(2)由正弦定理

故
因为


所以
考查方向
解题思路
该题解题思路如下
1)利用倍角公式
2)利用特殊角的三角函数求值得到角A,
3)使用正弦定理,进行边角之间的转换
4)根据角的取值范围得到答案
易错点
该题易于忽略了对A的范围的判断,该题属于中档题
在



17.求
18.若




正确答案
(1)
解析
试题分析:本题属于解三角形问题,属于基础题,主要考查两个定理的应用以及三角形的面积公式。具体解答步骤如下:
(Ⅰ)由正弦定理,
可得
所以
所以
因为


考查方向
解题思路
本题考查解三解形,解题步骤如下:
1)利用正弦定理及三角恒等变换求出C。
2)通过面积公式及
3)根据a,b的两组解分别求

易错点
1、利用余弦定理增加运算量; 2、第二问解三角形时遗漏一组解。
正确答案
(2)

解析
试题分析:本题属于解三角形问题,属于基础题,主要考查两个定理的应用以及三角形的面积公式。具体解答步骤如下:
(Ⅱ)解法一:由已知
所以


当

所以
所以


因为

在

当
所以

(Ⅱ)解法二:在


因为

由已知

又
解得
考查方向
解题思路
本题考查解三解形,解题步骤如下:
1)利用正弦定理及三角恒等变换求出C。
2)通过面积公式及
3)根据a,b的两组解分别求

易错点
1、利用余弦定理增加运算量; 2、第二问解三角形时遗漏一组解。
在△ABC中,已知a,b, c分别是角A,B,C的对边,且满足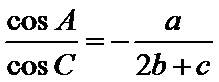
17.求角A的大小;
18.若a=2,求△ABC的周长的取值范围.
正确答案
(1)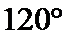
解析
(1)由正弦定理,得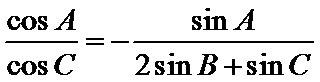
∴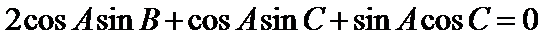
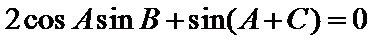
∵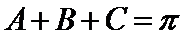
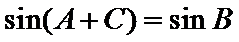
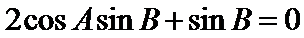
∵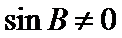
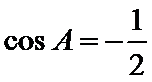
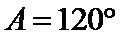
考查方向
解题思路
(1)利用已知条件和正弦定理求出角A(2)利用(1)中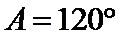
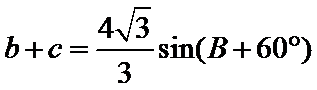
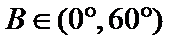
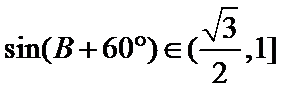
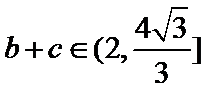
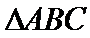
易错点
通过正弦定理表示三边即周长,易忽视角的范围出错。
正确答案
(2)
解析
(2)由正弦定理,得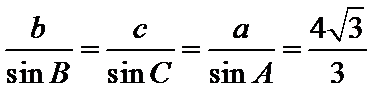
∴
=
=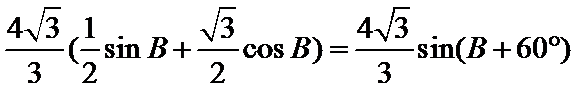
∵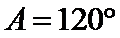
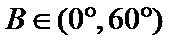
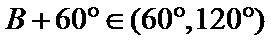
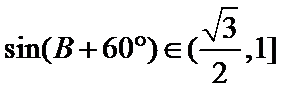
∴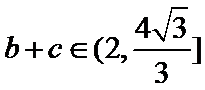
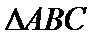
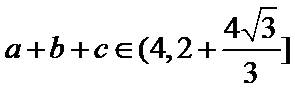
考查方向
解题思路
(1)利用已知条件和正弦定理求出角A(2)利用(1)中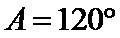
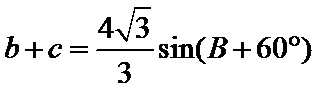
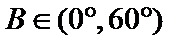
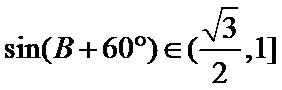
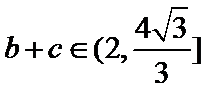
易错点
通过正弦定理表示三边即周长,易忽视角的范围出错。
5. 在




正确答案
解析
由正弦定理得



考查方向
解题思路
1.先利用正弦定理求出角C;2.利用大边对大角求出角C的准确值。
易错点
1.不知道应该用什么定理;2.不会根据大边对大角舍去一个角,导致结果出错。
知识点
6.在


正确答案
解析


考查方向
解题思路
根据所给条件,求出其他同角三角函数值
易错点
计算错误,忽略取值正负
知识点
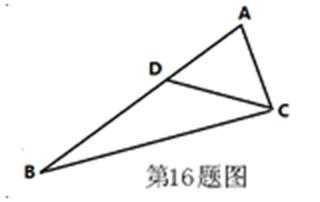
△ABC中,
17.求BC的长;
18.求△DBC的面积。
正确答案
3
解析
解∵cos∠ABC
在△ABC中,设BC=a,AC=3b ∴9b2=
在△ABD中, cos∠ADB=
在△BDC中, cos∠BDC=
cos∠ADB=-cos∠BDC


由①②
考查方向
解题思路
利用角的关系,利用余弦定理得到边的关系,通过解方程求得BC长。
易错点
含有a的方程不易处理。
正确答案
解析
解

考查方向
解题思路
利用角的关系,利用余弦定理得到边的关系,通过解方程求得BC长。
易错点
含有a的方程不易处理。
如图,在平面四边形





17.求
18.求
正确答案
(1) 
解析
(Ⅰ)在

即


由正
考查方向
解题思路
先利用余弦定理求出
易错点
不知道该在哪个三角形中使用什么定理;
正确答案
;(2)
解析
(Ⅱ)由(Ⅰ)有:

所以
由正弦定理得:
考查方向
解题思路
利用第(1)问的结论求出
易错点
意识不到
如图所示,在四边形





16.求△
17.若

正确答案
见解析
解析
(Ⅰ)
因为

所以△ACD的面积
考查方向
解题思路
利用已知条件求出∠D角的正弦函数值,然后求
易错点
主要易错于计算出错,
正确答案
见解析
解析
(Ⅱ)在△ACD中,
所以
在△ABC中,
把已知条件代入并化简得:

考查方向
解题思路
利用余弦定理求出AC,通过
易错点
主要易错于计算出错,
16.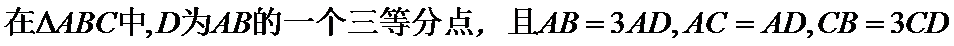
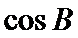
正确答案
解析
令AC=AD=1,CD=x > 0 , 则 AB=3 , BC= 3x ,
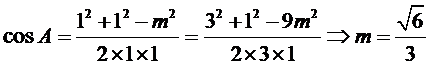
考查方向
解题思路
1.先设出题中需要的线段的长度;
2.根据余弦定理求出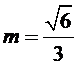
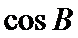
易错点
1.不会设出长度解决问题;
2.不会利用角A的余弦构造方程解方程。
知识点
在△ABC中,已知AB=2,AC=3,A=60°.
17.求BC的长;
18.求sin2C的值.
正确答案
解析
(1)由余弦定理可得:BC2=AB2+AC2﹣2AB•ACcosA=4+8﹣2×2×3×
所以BC=
考查方向
解题思路
直接利用余弦定理求解即可。
易错点
本题考查余弦定理的应用,正弦定理的应用,在计算时易错。
正确答案
解析
由正弦定理可得:



∵AB<BC,∴C为锐角,
则cosC=


因此sin2C=2sinCcosC=2×

考查方向
解题思路
利用正弦定理求出C的正弦函数值,然后利用二倍角公式求解即可.
易错点
本题考查二倍角的三角函数,在限制角的范围过程中易错。
扫码查看完整答案与解析