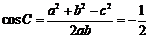三角函数与三角恒等变换_章节学习

1

题型：填空题

|

填空题 · 14 分

在中，内角所对的边分别为，已知

（Ⅰ）证明：

（Ⅱ）若的面积，求角A的大小.

正确答案

（I）由正弦定理得，

故，

于是．

又，，故，所以

或，

因此（舍去）或，

所以，．

（II）由得，故有

，

因，得．

又，，所以．

当时，；

当时，．

综上，或．

知识点

三角形中的几何计算

1

题型：简答题

|

简答题 · 4 分

9. 已知的三边长为，则该三角形的外接圆半径等于________________

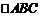
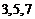
正确答案

解析

，

∴

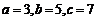
知识点

三角形中的几何计算解三角形的实际应用

1

题型：简答题

|

简答题 · 12 分

17.△ABC的内角A，B，C的对边分别别为a，b，c，已知

（I）求C；

（II）若的面积为，求△ABC的周长．

正确答案

解（Ⅰ）∵2cos C（acosB+bcosA）=C

∴2cos C（sinAcos B+sinBcosA）=sinC

∴2cosC sin(A+B)=sinC

∴2cosC sinC =sin C

∴

(Ⅱ) ∵△ABC面积为且

∴即

∴

∵a+b=5

∴a+b+c=5+

∴△ABC周长为5+.

知识点

正弦定理的应用余弦定理的应用三角形中的几何计算

1

题型：简答题

|

简答题 · 12 分

在△ABC中，角A,B,C所对的边分别是a,b,c,且.

19.证明：；

20.若，求.

第(1)小题正确答案及相关解析

正确答案

（Ⅰ）根据正弦定理，可设===k(k>0)．

则a=ksin A，b=ksin B，c=ksin C．

代入+=中，有

+=，变形可得

sin Asin B=sin Acos B+cos Asin B=sin(A+B)．

在△ABC中，由A+B+C=π，有sin(A+B)=sin(π–C)=sin C，

所以sin Asin B=sin C．

解析

（I）证明：由正弦定理可知原式可以化解为

∵和为三角形内角 , ∴则，两边同时乘以，可得由和角公式可知，原式得证。

考查方向

本题主要考查了正弦定理、余弦定理、商数关系、平方关系.考查学生的分析问题的能力和计算能力

解题思路

本题考查正弦定理、余弦定理、商数关系等基础知识，考查学生的分析问题的能力和计算能力.在解三角形的应用中，凡是遇到等式中有边又有角时，可用正弦定理进行边角互化，一种是化为三角函数问题，一般是化为代数式变形问题．在角的变化过程中注意三角形的内角和为这个结论，否则难以得出结论．

易错点

本题考查正弦定理、余弦定理、商数关系等基础知识，在用化边为角的技巧应用中有时会发生错误。

第(2)小题正确答案及相关解析

正确答案

（Ⅱ）4.

解析

（II）由题,根据余弦定理可知，

∵为为三角形内角，，

则，即由（I）可知，∴ ∴

考查方向

本题主要考查了正弦定理、余弦定理、商数关系、平方关系.考查学生的分析问题的能力和计算能力

解题思路

本题考查正弦定理、余弦定理、商数关系等基础知识，考查学生的分析问题的能力和计算能力.在解三角形的应用中，凡是遇到等式中有边又有角时，可用正弦定理进行边角互化，一种是化为三角函数问题，一般是化为代数式变形问题．在角的变化过程中注意三角形的内角和为这个结论，否则难以得出结论．

易错点

本题考查正弦定理、余弦定理、商数关系等基础知识，在用化边为角的技巧应用中有时会发生错误。

1

题型：填空题

|

填空题 · 5 分

13．在中，内角所对的边分别为，已知的面积为，则的值为 .

正确答案

8

解析

因为，所以，

又，解方程组得，由余弦定理得

，所以.

考查方向

1.同角三角函数关系；2.三角形面积公式；3.余弦定理.

解题思路

根据1.同角三角函数关系；2.三角形面积公式；3.余弦定理.结合已知条件构造方程组解出即可。

易错点

定理不熟悉。

知识点

正弦定理余弦定理三角形中的几何计算

1

题型：简答题

|

简答题 · 12 分

16.（本小题满分12分）

在△ABC中，角A，B，C的对边分别为a，b，c，已知

（Ⅰ）证明：a+b=2c;

（Ⅱ）求cosC的最小值.

正确答案

解析：由题意知，

化简得，

即.

因为,

所以.

从而.

由正弦定理得.

由知,

所以，

当且仅当时，等号成立.

故的最小值为.

考查方向

两角和的正弦公式、正切公式、正弦定理、余弦定理及基本不等式.

教师点评

知识点

三角形中的几何计算

1

题型：填空题

|

填空题 · 12 分

（本小题满分12分）

在△ABC中，角A,B,C所对的边分别是a,b,c,且.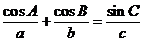

（I）证明：；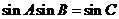

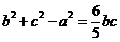
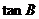
（II）若，求.

正确答案

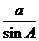
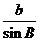
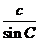
（Ⅰ）根据正弦定理，可设===k(k>0)．

则a=ksin A，b=ksin B，c=ksin C．

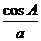
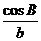
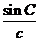
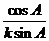
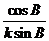
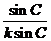
代入+=中，有

+=，变形可得

sin Asin B=sin Acos B+cos Asin B=sin(A+B)．

在△ABC中，由A+B+C=π，有sin(A+B)=sin(π–C)=sin C，

所以sin Asin B=sin C．

（Ⅱ）由已知，b2+c2–a2=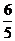bc，根据余弦定理，有

cos A==．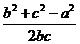

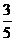
所以sin A==．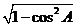

由（Ⅰ），sin Asin B=sin Acos B+cos Asin B，

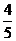
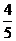
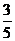
所以sin B=cos B+sin B，

故tan B=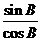=4．

知识点

正弦定理的应用余弦定理的应用三角形中的几何计算

1

题型：填空题

|

填空题 · 4 分

12．若锐角的面积为，且，则等于________．

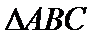
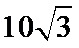
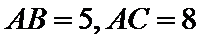
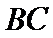
正确答案

解析

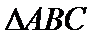
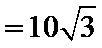
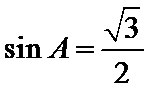
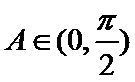
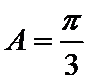
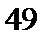
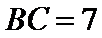
由已知得的面积为，所以，，所以．由余弦定理得，．

考查方向

1、三角形面积公式；2、余弦定理．

解题思路

利用三角形的面积公式求出A，再利用余弦定理求出BC.

易错点

计算能力弱，不会用余弦定理求三角形的面积

知识点

正弦定理余弦定理三角形中的几何计算

1

题型：填空题

|

填空题 · 5 分

16．在平面四边形ABCD中，∠A=∠B=∠C=75°，BC=2，则AB的取值范围是 .

正确答案

（，）.

解析

如图所示，延长BA，CD交于E，平移AD，当A与D重合与E点时，AB最长，在△BCE中，∠B=∠C=75°，∠E=30°，BC=2，由正弦定理可得，即，解得=，平移AD ，当D与C重合时，AB最短，此时与AB交于F，在△BCF中，∠B=∠BFC=75°，∠FCB=30°，由正弦定理知，，即，解得BF=，所以AB的取值范围为（，）.

考查方向

正余弦定理；数形结合思想

解题思路

本题可对边进行延长，由正弦定理求出BE然后求出BF,即可得到AB的范围。

易错点

本题在综合应用正余弦定理时易错。

知识点

正弦定理余弦定理三角形中的几何计算

1

题型：填空题

|

填空题 · 5 分

11．已知菱形的边长为2，，点分别在边上，，若，则的值为___________

正确答案

2

解析

由得：

考查方向

本题主要考查了平面向量的应用。

解题思路

本题考查运用平面向量在几何中的应用，解题步骤如下：建立如图所示直角坐标系，

则，由得：

易错点

本题必须注意审题，忽视则会出现错误。

知识点

三角形中的几何计算平面向量数量积的运算向量在几何中的应用

1

题型：简答题

|

简答题 · 12 分

在中，三个内角所对的边分别为，已知函数为偶函数，.

17.求；

18.若，求的面积.

第(1)小题正确答案及相关解析

正确答案

解析

由为偶函数可知，所以

又，故

所以

考查方向

本题考查了三角函数的变换和解三角形，属于常考题。

易错点

分类讨论角度。

第(2)小题正确答案及相关解析

正确答案

当时，的面积，当时，的面积

解析

，

当时，的面积，当时，的面积。

考查方向

本题考查了三角函数的变换和解三角形，属于常考题。

易错点

分类讨论角度。

1

题型：填空题

|

填空题 · 5 分

11．如图，在中，，，，则的值为________.

正确答案

解析

说明D在线段BC上，且是靠近B的一个三等分点，以向量, 为一组基底，表示出向量的数量积，即可算出的值为。

考查方向

本题主要考查了平面向量的数量积,在近几年的各省高考题出现的频率较高，常与三角恒等变形公式，向量的运算等知识点交汇命题。

解题思路

平面向量的数量积计算问题，往往有两种形式，一种是数量积的定义，而是利用数量积的坐标运算公式，涉及几何图形的问题，可利用几何性质用一组已知基底数量积表示所求数量积。

易错点

1、本题易直接使用数量积的定义，而不知如何计算夹角。

2、不会选择一组基底，从而用向量的加减运算及利用几何性质用一组已知基底数量积表示所求数量积。

知识点

余弦定理三角形中的几何计算平面向量数量积的运算向量在几何中的应用

1

题型：简答题

|

简答题 · 12 分

已知分别是内角的对边，．

17.若，求；

18.若，且，求的面积．

第(1)小题正确答案及相关解析

正确答案

解析

试题分析：本题属于三角恒等变形和解三角形的基本问题，对结合想到余弦定理进行化简求解；由题设及正弦定理可得

又，可得由余弦定理可得．

考查方向

本题考查了正余弦定理在解三角形的应用和面积公式的求解；

解题思路

本题考查解三角形，解题步骤如下：对结合想到余弦定理进行化简求解；

易错点

对结合的化简方向的选择

第(2)小题正确答案及相关解析

正确答案

；

解析

试题分析：本题属于三角恒等变形和解三角形的基本问题，由方程思想求解出边长再算出面积；由17可知．∵，由勾股定理得．故，得．∴的面积为．

考查方向

本题考查了正余弦定理在解三角形的应用和面积公式的求解；

解题思路

本题考查解三角形，解题步骤如下：由方程思想求解出边长再算出面积。

易错点

根据条件合理选择定理来解三角形。

1

题型：填空题

|

填空题 · 5 分

13．△ABC的内角A，B，C的对边分别为a，b，c且ac＝，A＝，则B＝_______．

正确答案

解析

由ac＝，A＝及正弦定理得即化简得,又，联立解得所以B＝

考查方向

本题主要考查了正余定理及三角诱导公式，考查考生的运算能力。

解题思路

由ac＝，A＝及正弦定理得，再利用可算得从而得到B＝

易错点

忽视隐含条件

知识点

三角形中的几何计算

1

题型：简答题

|

简答题 · 14 分

在中，角的对边分别是，向量与互相垂直.

16.求的值；

17.若，求的面积．

第(1)小题正确答案及相关解析

正确答案

；

解析

试题分析：本题属于向量的坐标运算、正余弦定理及三角形的面积公式的综合应用问题，属于简单题，只要掌握相关的知识，即可解决本题，解析如下：因为，所以，所以，所以，而，所以.

考查方向

本题考查了向量的坐标运算、正余弦定理的综合应用等知识点。

解题思路

利用向量得出数量积为零，整理即可求出的值；

易错点

正确答案

．

解析

试题分析：本题属于向量的坐标运算、正余弦定理及三角形的面积公式的综合应用问题，属于简单题，只要掌握相关的知识，即可解决本题，解析如下：

由余弦定理得，，

化简得，，解得，3或5，而，又,

故或.

考查方向

本题考查了向量的坐标运算、正余弦定理的综合应用等知识点。

解题思路

利用余弦定理求出a边，在利用面积公式即可求出的面积．

热门试卷

正确答案

知识点

正确答案

解析

知识点

正确答案

知识点

正确答案

解析

考查方向

解题思路

易错点

正确答案

解析

考查方向

解题思路

易错点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

考查方向

教师点评

知识点

正确答案

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

易错点

正确答案

解析

考查方向

易错点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

正确答案

解析

考查方向

解题思路

易错点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析