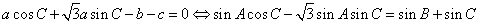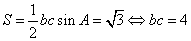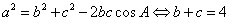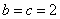- 三角函数与三角恒等变换
- 共3475题
如图,ABCD是边长为10海里的正方形海域.现有一架飞机在该海域失事,两艘海事搜救船在










(1)试建立


(2)求

正确答案
(1)
解析
(1)
(2)令







此时,
知识点
已知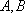

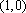
(1)当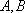

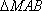
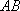
(2)当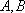

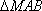
正确答案
见解析
解析
(1) 设
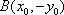
因为
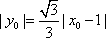
又点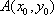
所以 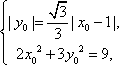
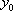
得到 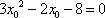
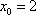
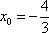
当

当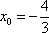
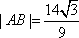
{说明:若少一种情况扣2分}
(2)法1:根据题意可知,直线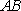
设直线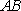
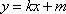
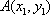
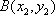
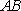
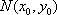
联立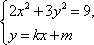


由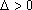
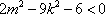
所以
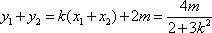
所以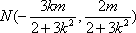
如果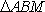
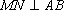
所以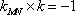
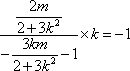
化简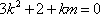
由②得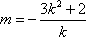
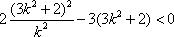
化简得 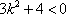
{此步化简成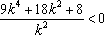
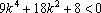

故
法2:设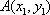
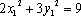
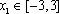
所以 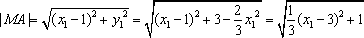
设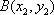
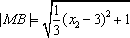
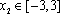
因为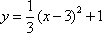

所以,有
因为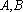

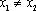
所以
所以
知识点
在










(1)求边
(2)求
正确答案
(1)
(2)
解析
(1)由

所以
由

所以
(2)由

所以
所以
知识点
将边长为1m正三角形薄片,沿一条平行于底边的直线剪成两块,其中一块是梯形,记
正确答案
解析
考查函数中的建模应用,等价转化思想。一题多解。
设剪成的小正三角形的边长为
(方法一)利用导数求函数最小值。


当



故当

(方法二)利用函数的方法求最小值。
令
故当

知识点
已知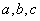
(1)求
(2)若
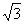
正确答案
(1)
(2)
解析
(1)由正弦定理得:
(2)
解得:
知识点
在

sinB=
(1)求tanC的值;
(2)若a=

正确答案
(1) 

解析
本题主要考察三角恒等变换,正弦定理,余弦定理及三角形面积求法等知识点。
(1)∵cosA=

又
=

整理得:tanC=
(2)由图辅助三角形知:sinC=
又由正弦定理知:
故
对角A运用余弦定理:cosA=
解(1) (2)得:

∴

知识点
某兴趣小组测量电视塔AE的高度H(单位:m),如示意图,垂直放置的标杆BC的高度h=4m,仰角∠ABE=

(1)该小组已经测得一组



(2)该小组分析若干测得的数据后,认为适当调整标杆到电视塔的距离d(单位:m),使



正确答案
(1)124m.
(2)
解析
(1)


AD—AB=DB,故得

因此,算出的电视塔的高度H是124m。
(2)由题设知



故当

因为




故所求的

知识点
如图,某人在垂直于水平地面ABC的墙面前的点A处进行射击训练.已知点A到墙面的距离为AB,某目标点P沿墙面上的射击线CM移动,此人为了准确瞄准目标点P,需计算由点A观察点P的仰角





正确答案
解析
∵AB=15cm,AC=25cm,∠ABC=90°,∴BC=20cm,
过P作PP′⊥BC,交BC于P′,
1当P在线段BC上时,连接AP′,则
设BP′=x,则CP′=20-x,(
由∠BCM=30°,得
在直角△ABP′中,
∴
令
∴x=0时,
2当P在线段CB的延长线上时,连接AP′,则
设BP′=x,则CP′=20+x,(
由∠BCM=30°,得
在直角△ABP′中,
∴
令

所以,当


所以当
此时

综合1,2可知
知识点
已知点O(0,0),A(0,b),B(a,a3),若△OAB为直角三角形,则必有( )。
正确答案
解析
若B为直角,则
即a2+a3(a3-b)=0,
又a≠0,故
若A为直角,则
若O为直角,则不可能,故b-a3=0或b-a3-
知识点
气象台预报,距离


问:(1)从台风形成起经过3小时,
(2)从台风形成起经过多少小时,S岛开始受到台风的影响?持续时间多久?(精确到0.1小时)
正确答案
(1)是(2)4.9小时
解析
(1) 设台风中心经过3小时到达点B,由题意,在



所以,经过3小时S岛已经受到了影响.
(2)可设台风中心经过t小时到达点B,由题意得,



若S岛受到台风影响,则有 

化简整理得


知识点
已知条件

① 


③ 


则其中是
正确答案
①③④
解析
略
知识点
某人沿一条折线段组成的小路前进,从










试画出大致示意图,并计算出从

正确答案
见解析
解析
示意图,如图所示,
连接AC,在△ABC中,∠ABC=50°+(180°-110°)=120°,
又AB=BC=3,∴∠BAC=∠BCA=30°
由余弦定理可得
在△ACD中,∠ACD=360°-140°-(70°+30°)=120°,CD=3
由余弦定理得AD=
=

由正弦定理得sin∠CAD=
∴∠CAD=45°,于是AD的方位角为50°+30°+45°=125°,
所以,从A到D的方位角是125°,距离为
知识点
如图2,一条河的两岸平行,河的宽度
一艘客船从码头

已知

驶完航程所用最短时间为
的速度大小为
正确答案
解析
略
知识点
已知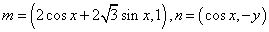
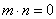
(1)将y表示为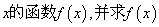
(2)已知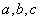
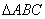

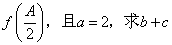
正确答案
见解析。
解析
知识点
已知函数

(1)求函数
(2)已知







正确答案
见解析。
解析
(1)



由





(2)∵


∵


即

由余弦定理

即

∴
知识点
扫码查看完整答案与解析