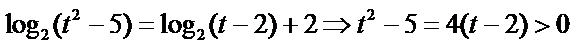- 对数的运算性质
- 共69题
20.若
（1） 求
（2）若不等式
正确答案
（1） ∵
∴ 
∴ a = 2或a = 1（舍）
又 ∵
∴ 
∴ 
∴ 当
（2）由
∴
∴
∴ 
由
∴
∴
∴
解析
解析已在路上飞奔，马上就到！
知识点
15． 有四个命题：
①函数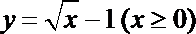
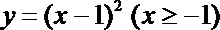
②函数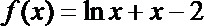
③函数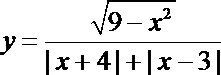
④若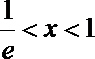
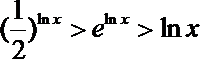
其中真命题的序号是________．
正确答案
③④
解析
解析已在路上飞奔，马上就到！
知识点
5.已知数列{an}满足a1=1,an=logn（n+1）（n≥2,n∈N*）.定义:使乘积a1·a2·…·ak为正整数的k（k∈N）叫作“酷数”.则在[1,2016]内所有“酷数”的和为（ ）.
正确答案
解析
∵an=logn(n+1),∴a1·a2·a3·…·an=1×log23×log34×…×logn(n+1)=
则在[1,2016]内所有“酷数”的和为21-1+22-1+…+210-1=
知识点
3.在等差数列{an}中,a3+a8=4,则log2（
正确答案
解析
∵在等差数列{an}中,a3+a8=4,
∴a1+a10=a2+a9=a4+a7=a5+a6=a3+a8=4,
∴a1+a2+…+a10=(a1+a10)+(a2+a9)+(a3+a8)+(a4+a7)+(a5+a6)=5(a3+a8)=20,则log2(
知识点
2．方程
正确答案
解析
∵
∴方程
考查方向
本题主要考查了对数方程的解法，考查学生计算能力，属于容易题．
易错点
在对数方程的求解中，将对数式转化成指数式的过程中，特别要注意对数式中的底数、真数、对数与指数式中的底数、幂、指数的对应关系．
知识点
7．方程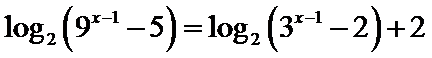
正确答案
解析
设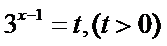
知识点
2.设函数
正确答案
解析
考查方向
解题思路
1、先求
2、
易错点
1.不会将
2.忘记公式
知识点
5.设函数
A
B6
C9
D12
正确答案
知识点
8．正项等比数列{
A1
B2
C
D－1
正确答案
解析
考查方向
本题主要考查极值和数列、对数运算
解题思路
1、求出a1,a4031；
2、求出a2016，即可得到结果。B选项不正确，C选项不正确，D选项不正确，所以选A选项。
易错点
本题易在求a2016时发生错误。
知识点
4．函数
A
B
C
D
正确答案
解析
故选A
考查方向
分段函数、指数函数对数函数
解题思路
根据题意，层层带入到函数中
易错点
分段函数的函数定义域弄混淆
知识点
扫码查看完整答案与解析