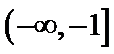求函数的值
共92题

· 求函数的值

求函数的值
共92题

热门试卷

X 查看更多试卷

题型：单选题

单选题 · 5 分

7.已知函数，的值为（）

正确答案

解析

，

∴=

∴所以选项A为正确选项

考查方向

本题主要考查了分段函数的性质,属于基础题，是高考的热点

解题思路

先判断范围，代入相应解析式即可

易错点

本题易在分段函数的应用错误，判断不出变量范围

知识点

函数的图象与图象变化求函数的值

题型：单选题

单选题 · 5 分

10.已知函数，且fA.=-3，则f（6-a）=( )

A-

B-

C-

D-

正确答案

知识点

求函数的值对数的运算性质

题型：单选题

单选题 · 5 分

6.已知函数是周期为的奇函数，当时，，则

正确答案

解析

由函数是周期为的奇函数得，

故

考查方向

本题主要考查函数的奇偶性和周期性以及对数的运算性质等知识，意在考查考生的转化能力和运算求解能力。

解题思路

利用函数为周期为的奇函数将化简为；利用题中给出的解析式得到。

易错点

不会将化简到给定的区间；利用对数的运算性质运算时出错。

知识点

函数奇偶性的性质函数的周期性求函数的值

题型：单选题

单选题 · 5 分

6.定义在上的函数满足，且当时，=，

则（）

正确答案

解析

即自变量加1，y值变为原来的一半

考查方向

本题主要考察了函数的基本性质，考察了抽象函数及其应用，本题较简单

解题思路

该题是常规题，主要是得到即自变量加1，y值变为原来的一半，所以得到对应区间，带入解析式得到结果

易错点

本题易错在变换过程系数的变化

知识点

函数的周期性求函数的值

题型：填空题

填空题 · 5 分

13．已知函数，则　　　　　.

正确答案

解析

．

考查方向

本题主要考查了分段函数与复合函数求值的问题。

解题思路

本题考查采用正确求分段函数的值的能力，解题步骤如下：从内到外一次求出即可。

易错点

本题必须在求值的时候只能带入相应的表达式中去求，忽视则会出现错误。

知识点

分段函数的解析式求法及其图象的作法求函数的值

题型：单选题

单选题 · 5 分

3．设函数，则（）

D12

正确答案

解析

由题设知：。所以选C。

考查方向

本题主要考查了由函数的解析式求函数值的问题。

解题思路

本题考查由自变量的范围确定用对应的解析式。

易错点

本题必须注意自变量所在范围的问题，忽视则会出现错误。

知识点

分段函数的解析式求法及其图象的作法求函数的值

题型：填空题

填空题 · 5 分

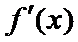
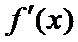
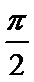
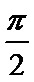
16．已知函数y＝f（x）为R上的偶函数，y＝f（x）的导数为，且当x∈（－∞，0]时，不等式f（x）＋x·＜0成立，若a·f（a）≥sinθ·f（sinθ）对一切θ∈

[－，]恒成立，则实数a的取值范围是__________．

正确答案

解析

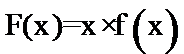
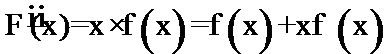
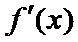
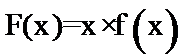
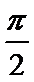
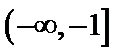
构造函数，则，在当x∈（－∞，0]时，不等式f（x）＋x·＜0成立，而由于函数y＝f（x）为R上的偶函数所以函数是奇函数，对称的区间上函数的单调性相同，所以a·f（a）≥sinθ·f（sinθ）对一切θ∈[－，]恒成立，只要满足a的取值范围。

考查方向

函数的导数与函数的单调性以及求参数的取值范围问题。

解题思路

先构造函数，然后利用所构造的函数将已知要求的参数的取值范围转化为求函数的最值问题。

易错点

不知道构造函数来解答。

知识点

求函数的值利用导数研究函数的单调性利用导数求函数的极值

题型：填空题

填空题 · 6 分

11.设函数，则= ▲ ，若[，]，则

实数的取值范围是 ▲ .

正确答案

，

解析

考查方向

本题考查了分段函数问题，考查对数函数的性质，复合函数的性质，是一道中档题

解题思路

1、根据对数恒等式直接得出结果

2、在不同区间上解不等式后取并集

易错点

主要易错于对分段函数求不等式理解出错

知识点

分段函数的解析式求法及其图象的作法求函数的值

题型：填空题

填空题 · 5 分

13.若函数，则．

正确答案

解析

。

考查方向

分段函数求函数值。

解题思路

本题考查分段函数求函数值的能力，解题步骤如下：先求f（5），再继续下去直到求出其值。

易错点

带错解析式。

知识点

分段函数的解析式求法及其图象的作法求函数的值

题型：填空题

填空题 · 5 分

正确答案

知识点

求函数的值导数的运算

继续学习学习下一知识点

下一知识点 : 函数恒成立、存在、无解问题

百度题库 > 高考 > 文科数学 > 求函数的值

扫码查看完整答案与解析