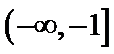- 求函数的值
- 共92题
1
题型:
单选题
|
7.已知函数

正确答案
A
解析

∴
∴所以选项A为正确选项
考查方向
本题主要考查了分段函数的性质,属于基础题,是高考的热点
解题思路
先判断
易错点
本题易在分段函数的应用错误,判断不出变量范围
知识点
函数的图象与图象变化求函数的值
1
题型:
单选题
|
10.已知函数
正确答案
A
知识点
求函数的值对数的运算性质
1
题型:
单选题
|
3.设函数

正确答案
C
解析
由题设知:
考查方向
本题主要考查了由函数的解析式求函数值的问题。
解题思路
本题考查由自变量的范围确定用对应的解析式。
易错点
本题必须注意自变量所在范围的问题,忽视则会出现错误。
知识点
分段函数的解析式求法及其图象的作法求函数的值
1
题型:填空题
|
16.已知函数y=f(x)为R上的偶函数,y=f(x)的导数为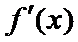
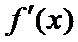
[-
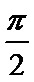
正确答案
解析
构造函数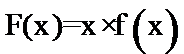
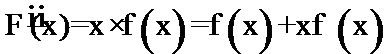
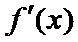
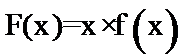
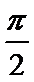

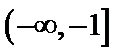
考查方向
函数的导数与函数的单调性以及求参数的取值范围问题。
解题思路
先构造函数,然后利用所构造的函数将已知要求的参数的取值范围转化为求函数的最值问题。
易错点
不知道构造函数来解答。
知识点
求函数的值利用导数研究函数的单调性利用导数求函数的极值
1
题型:填空题
|
正确答案
2
知识点
求函数的值导数的运算
下一知识点 : 函数恒成立、存在、无解问题
扫码查看完整答案与解析