- 数量积表示两个向量的夹角
- 共88题
12.在平面直角坐标系中,已知A(1,0),B(0,-1),P是曲线

正确答案
解析
知识点
8.设O为坐标原点,P是以F为焦点的抛物线


正确答案
解析








考查方向
解题思路
本题考查抛物线的性质,结合题意要求,利用抛物线的参数方程表示出抛物线上点



易错点
本题考查抛物线的性质,用基本不等式时易错
知识点
15.平面直角坐标系xOy中,双曲线C1:
正确答案
解析
双曲线C1:

与抛物线C2:x2=2py联立,可得x=0或x=±
取A(


∵△OAB的垂心为C2的焦点,
∴

∴5a2=4b2,∴5a2=4(c2﹣a2)
∴e=


考查方向
解题思路
求出A的坐标,可得


易错点
双曲线的简单性质.菁优网版权所有
知识点
13.向量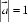
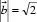
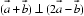

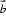
正确答案
解析
由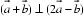
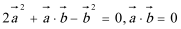

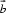
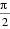
考查方向
本题主要考查了平面向量的夹角公式。
解题思路
本题考查平面向量的夹角公式,解题步骤如下:
1、利用垂直条件求出数量积。
2、利用夹角公式求解.
易错点
本题必须注意数量积的公式。
知识点
3.平面向量
正确答案
解析




考查方向
本题主要考查两个向量的数量积的定义,求向量的模的方法,属于中档题
解题思路
先求出
易错点
数量积表示两个向量的夹角,向量的模
知识点
扫码查看完整答案与解析