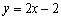函数恒成立问题
共47题

· 函数恒成立问题

函数恒成立问题
共47题

热门试卷

X 查看更多试卷

题型：简答题

简答题 · 12 分

17．若对满足的任意实数，使得不等式恒成立，求实数的取值范围。

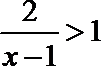
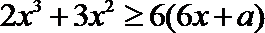
正确答案

解析

解析已在路上飞奔，马上就到！

知识点

函数恒成立问题

题型：填空题

填空题 · 5 分

若存在实常数和，使得函数和对其定义域上的任意实数分别满足：和，则称直线为和的“隔离直线”，已知函数和函数，那么函数和函数的隔离直线方程为_________。

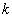
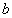
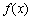
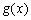
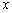
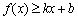
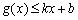
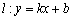
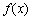
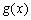
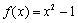
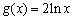
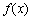
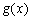
正确答案

解析

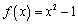
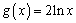
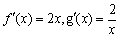
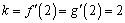
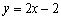
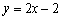
有题可知函数与函数有公共点，由隔离直线的定义可知只有二者的公切线才能满足，，可知，可知直线方程为，故答案为。

知识点

函数恒成立问题直线的两点式方程直线的一般式方程

题型：简答题

简答题 · 14 分

已知函数

（1）若曲线与曲线相交，且在交点处有共同的切线，求a的值和该切线方程；

（2）设函数，当存在最小值时，求其最小值的解析式；

（3）对（2）中的和任意的，证明：

正确答案

见解析。

解析

（1），

由已知得解得，

∴ 两条直线交点的坐标为，切线的斜率为，

∴ 切线的方程为

（2）由条件知

∴

（ⅰ）当a>0时，令，解得，

∴ 当时，在上递减；

当时，在上递增

∴是在上的唯一极值点，从而也是的最小值点

∴最小值

（ⅱ）当时，在上递增，无最小值，

故的最小值的解析式为

（3）由（2）知

对任意的

①

②

③

故由①②③得

知识点

函数恒成立问题导数的几何意义导数的运算不等式的性质

题型：单选题

单选题 · 5 分

已知函数，定义函数给出下列命题：

①；

②函数是奇函数；

③当时，若，，总有成立。

其中所有正确命题的序号是

A②

B①②

C③

D②③

正确答案

解析

略

知识点

命题的真假判断与应用函数奇偶性的判断函数恒成立问题

题型：简答题

简答题 · 13 分

已知函数，其中.

（1）若对一切，恒成立，求的取值集合.

（2）在函数的图像上取定两点，记直线的斜率为.问：是否存在，使成立？若存在，求的取值范围；若不存在，请说明理由.

正确答案

见解析

解析

（1）若，则对一切，，这与题设矛盾，又，

故.

而令

当时，单调递减；当时，单调递增，故当时，取最小值

于是对一切恒成立，当且仅当

.①

令则

当时，单调递增；当时，单调递减.

故当时，取最大值.因此，当且仅当即时，①式成立.

综上所述，的取值集合为.

（2）由题意知，

令则

令，则.

当时，单调递减；当时，单调递增.

故当，即

从而，又

所以

因为函数在区间上的图像是连续不断的一条曲线，所以存在，使，单调递增，故这样的是唯一的，且.故当且仅当时， .

综上所述，存在使成立.且的取值范围为.

知识点

函数的最值及其几何意义函数恒成立问题导数的几何意义导数的运算

继续学习棒棒哒，已是最后一个知识点

已完结

百度题库 > 高考 > 理科数学 > 函数恒成立问题

扫码查看完整答案与解析