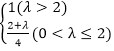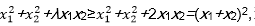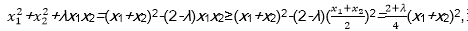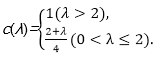函数恒成立问题
共47题

· 函数恒成立问题

函数恒成立问题
共47题

热门试卷

X 查看更多试卷

题型：填空题

填空题 · 5 分

16.已知函数.若当时,不等式>0恒成立,则实数m的取值范围是_________________.

正确答案

m≤-2

解析

令f(x)=(2-2-|x+2|)2,

要使f(x)=2+a有实根,

只需2+a是f(x)值域内的值.

∵f(x)的值域为[1,4),

∴1≤2+a<4,∴-1≤a<2.

知识点

函数恒成立问题不等式的应用

题型：填空题

填空题 · 5 分

9.若λ>0对于任意非负实数x1,x2都有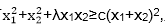则最大的常数c=c(λ)=________.

正确答案

解析

　(i)当λ>2时,

当且仅当x1=x2=0时等号成立.

(ii)当0<λ≤2时,

当且仅当x1=x2时等号成立.

由(i)(ii)知,

知识点

函数恒成立问题

题型：单选题

单选题 · 5 分

6.设f=3x-3-x+x3,若当t>0时,f（m+3t）+f（mt-t2）≤0恒成立,则实数m的取值范围是（　　）.

A（-∞,-1]

B[0,+∞）

C[-1,+∞）

D（-∞,0]

正确答案

解析

由题意知函数f是定义在R上的奇函数且为增函数,故f(m+3t)≤f(t2-mt),m+3t≤t2-mt对任意的t>0恒成立,即m≤对任意的t>0恒成立.令g(t)===(t+1)+-5≥-1,当且仅当t+1=,即t=1时等号成立,所以g(t)min=-1,故实数m的取值范围是(-∞,-1]

知识点

函数恒成立问题

题型：填空题

填空题 · 5 分

10.已知函数f(x)=loga(1+x)在区间[1,+∞)上恒有|f(x)|>2,则a的取值范围为　　　　.

正确答案

解析

若a>1,由于在区间[1,+∞)上,

得loga(1+x)>0,

因此，恒成立,

即loga(1+x)>2,得恒成立,

因为2≤x+1,那么a2<2,

结合a>1,得

若0<a<1,由于1+x>1,

得loga(1+x)<0,

因此,|f(x)|>2恒成立,

即

得a-2<x+1恒成立,

因为2≤x+1,那么a-2<2,

结合0<a<1,得<a<1.

综上得,a的取值范围为

知识点

函数恒成立问题对数函数的图像与性质对数函数的单调性与特殊点

题型：填空题

填空题 · 5 分

16.若函数的定义域为R,则实数m的取值范围为　　　　.

正确答案

解析

由,

设g(x)=x-ex,得g'(x)=1-ex,

显然x<0时,g'(x)>0,

此时函数g(x)递增;x>0时,g'(x)<0,

此时函数g(x)递减;于是当x=0时,

函数有最大值g(0)=-1,

于是函数g(x)的值域为(-∞,-1].

欲使x∈R时,

都有

则m的取值范围为(-1,+∞).

知识点

函数恒成立问题

继续学习棒棒哒，已是最后一个知识点

已完结

百度题库 > 高考 > 理科数学 > 函数恒成立问题

扫码查看完整答案与解析