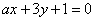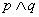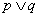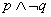- 两条直线平行的判定
- 共15题
9. 在△ABC中,a、b、c分别为∠A、∠B、∠C的对边,若a、b、c成等差数列,sinB=

正确答案
2
解析
解析已在路上飞奔,马上就到!
知识点
给出命题p:直线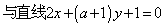
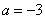
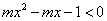
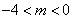
正确答案
解析
略
知识点
已知直线


(1)求a,b的值;
(2)若函数










设C1在点M处的切线的斜率为



正确答案
见解析
解析
解:(1)直线

又


(2)

∴

由


则

又
法一:令


因为





则

法二:令


因为


故



于是

故






知识点
在四棱锥



(1)求证:

(2)求证:
(3)若




正确答案
见解析
解析
(1)连接
由


又

所以

又
所以

(2) 证明:由
所以
由
又
所以
又
所以
(3)解法一:
在线段


如图,取


在四棱锥

所以
由(2)可知,
所以,
因为
所以
故在线段


由


解法二:
由

建立空间直角坐标系
由已知

则





由题意,若线段




所以,
故在线段



知识点
5.“




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析