- 直线、平面垂直的综合应用
- 共65题
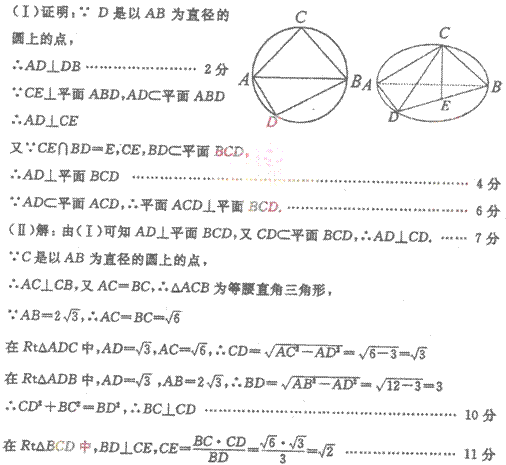
如图：C、D是以AB为直径的圆上两点，AB＝2AD＝
（1）求证：平面ACD⊥平面BCD；
（2）求三棱锥C－ABD的体积。
正确答案
见解析。
解析
知识点
已知矩形ABCD的顶点都在半径为4的球O的球面上，且AB=6.BC=2
正确答案
8
解析
由题意求出矩形的对角线的长，结合球的半径，球心到矩形的距离，满足勾股定理，求出棱锥的高，即可求出棱锥的体积。
解：矩形的对角线的长为：
所以棱锥O﹣ABCD的体积为：
故答案为：8
知识点
如图，已知平面
A
B
C
D
正确答案
解析
因为
设
在三角形中有
知识点
斜率为
A
B
C
D
正确答案
解析
略
知识点
如图，C、D是以AB为直径的圆上两点，AB=2AD=
（1）求证：AD⊥平面BCE；
（2）求证：AD∥平面CEF；
（3）求三棱锥A﹣CFD的体积。
正确答案
见解析。
解析
（1）证明：依题意：AD⊥BD
∵CE⊥平面ABD∴CE⊥AD
∵BD∩CE=E，∴AD⊥平面BCE。
（2）证明：Rt△BCE中，
∴BE=2
Rt△ABD中，
∴BD=3.
∴
∴AD∥EF∵AD在平面CEF外
∴AD∥平面CEF。
（3）解：由（2）知AD∥EF，AD⊥ED，且ED=BD﹣BE=1
∴F到AD的距离等于E到AD的距离，为1。
∴
∵CE⊥平面ABD
∴
知识点
扫码查看完整答案与解析