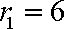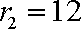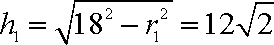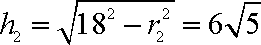- 直线、平面垂直的综合应用
- 共65题
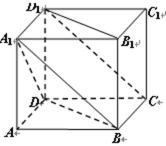
如图在四棱锥








(1)求证:
(2)求证:

(3)求四面体
正确答案
见解析
解析
解析:证明:(1)连接

(2) 
又


在





(3)由


知识点
如图(1)在等腰










(1)求证:

(2)求证:
(3)设三棱锥




正确答案
见解析
解析
(1)证明:如图:在△ABC中,由E、F分别是AC、BC中点,得EF//AB,
又AB

(2)∵平面

AD⊥CD, 且
∴



又∵
∴


∴
(3)由(2)可知



∴
又∵



∴三棱锥

三棱锥

∴三棱锥
∴
∴
知识点
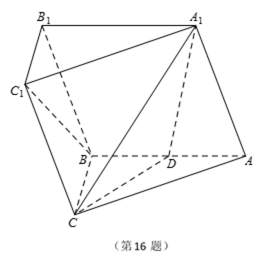
如图,在三棱柱





(1)求证:平面

(2)求证:

正确答案
见解析。
解析
(1)证明:∵ 

∴△



∵






∵



(2)证明:连结


∵三棱柱的侧面


在△




∵





知识点
如图,在五面体






(1)求证:
(2)求三棱锥
正确答案
见解析。
解析
(1)
因为




所以

又



所以
(2)在平面


因为




又



所以

所以

在直角三角形



因为




又由(1)知,



所以三棱锥

知识点
如图,在三棱柱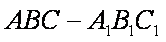
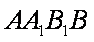
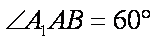

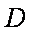
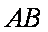
(1)求证:平面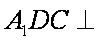
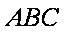
(2)求证: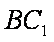
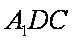
正确答案
见解析。
解析
(1)证明:∵ 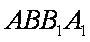

∴△

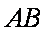
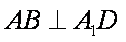
∵
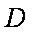

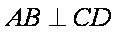
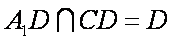
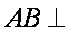

∵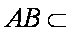

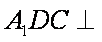
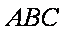
(2)证明:连结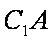
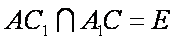
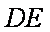
∵三棱柱的侧面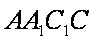
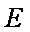
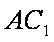
在△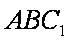
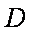
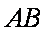
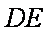
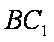
∵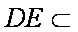

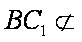
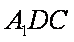
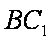
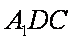
知识点
如右图,在底面为平行四边形的四棱柱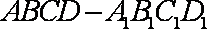

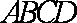
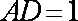
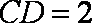
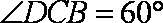
(1)求证:平面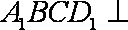
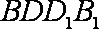
(2)若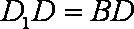
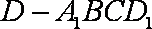
正确答案
见解析
解析
(1)证明: 在
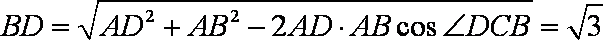
所以

又四边形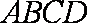

又
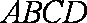
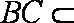
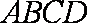
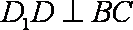
又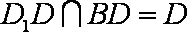
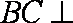
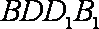
又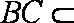
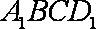
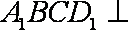
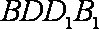
(2)连结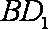
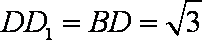
∴
∵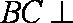
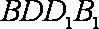
所以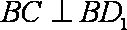
所以四边形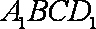
面积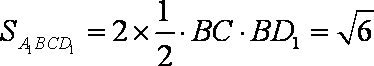
取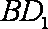
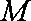
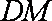
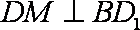
且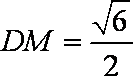
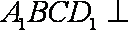
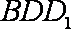
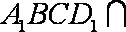
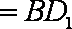
所以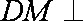
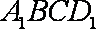
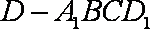
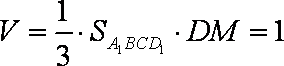
知识点
将一个半径为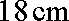

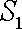
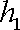
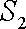
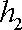
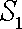
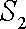
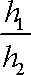
正确答案
见解析
解析
(1)因圆的面积为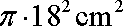
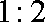
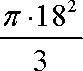
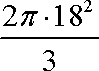
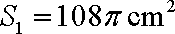
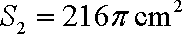
(2)较小圆锥的底面半径为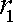
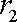
由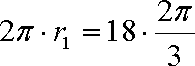


∴

∴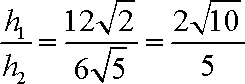
知识点




(1)求证:平面

(2)若在棱





正确答案
见解析。
解析
(1)
连AC,则AC⊥






∵ 


∵ 



∵ 


∵ 



(2)设



∵ 





∴ 
∴ 



知识点
已知等腰梯形PDCB中(如图1),PB=3,DC=1,PB=BC=
(1)证明:平面PAD⊥PCD;
(2)试在棱PB上确定一点M,使截面AMC
把几何体分成的两部分
正确答案
见解析。
解析
(1)证明:依题意知:
(2)
由(1)知
∴平面PAB⊥平面ABCD.
在PB上取一点M,作MN⊥AB,则MN⊥平面ABCD,
设MN=h
则
要使
知识点
如图,正△ABC的边长为4,CD是AB边上的高,E,F分别是AC和BC边的中点,现将△ABC沿CD翻折成直二面角A-DC-B。
(1)试判断直线AB与平面DEF的位置关系,并说明理由;
(2)求棱锥E-DFC的体积;
(3)在线段BC上是否存在一点P,使AP⊥DE?如果存在,求出
正确答案
见解析
解析
(1)AB∥平面DEF,理由如下:如图:在△ABC中,由E、F分别是AC、BC中点,得EF∥AB,
又AB⊄平面DEF,EF⊂平面DEF,∴AB∥平面DEF。
(2)∵AD⊥CD,BD⊥CD,将△ABC沿CD翻折成直二面角A-DC-B。
∴AD⊥BD ∴AD⊥平面BCD
取CD的中点M,这时EM∥AD ∴EM⊥平面BCD,EM=1,
(3)在线段BC上存在点P,使AP⊥DE
证明如下:在线段BC上取点P,使BP=BC/3, 过P作PQ⊥CD于Q,
∵AD⊥平面BCD ∴PQ⊥平面ACD
∴DQ=DC/3=2√3/3, ∴tan∠DAQ=DQ/AD═(2√3/3)/2=√3/3,
∴∠DAQ=30° 在等边△ADE中,∠DAQ=30° ∴AQ⊥DE
∵PQ⊥平面ACD ∴AP⊥DE,AQ∩AP=A
∴DE⊥平面APQ, ∴AP⊥DE,
此时BP=BC/3, ∴BP/BC=1/3。
知识点
扫码查看完整答案与解析