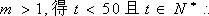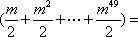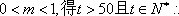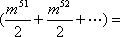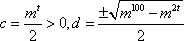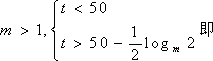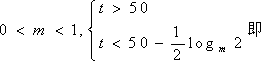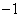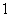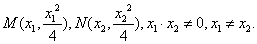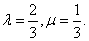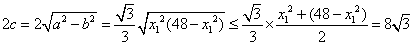- 数系的扩充和复数的引入
- 共721题
若复数



正确答案
解析
略
知识点
设i为虚数单位,则复数
正确答案
解析
解:

故选A。
知识点
设虚数
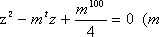
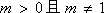

(1)求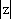
(2)当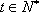

(3)设虚数


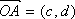
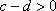

正确答案
见解析
解析
(1)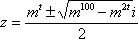
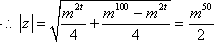
(或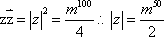
(2)
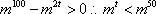

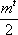
当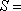
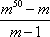
当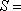
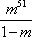
(3)
① 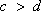
由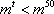
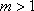
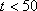
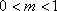
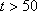
② 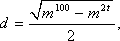

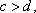
当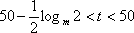
当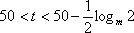
知识点
已知

正确答案
解析
略
知识点
i是虚数单位,则
正确答案
: 1﹣i
解析
∵


∴
故答案为:1﹣i
知识点
若复数
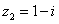
正确答案
解析
知识点
已知


正确答案
解析
略
知识点
计算:i(1+i)2=( )
正确答案
解析
i(1+i)2=i(1+2i+i2)=i(1﹣1+2i)=2i2=﹣2。
故选A
知识点
已知复数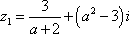
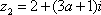
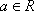

(1)若复数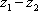

(2)若虚数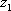
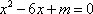

正确答案
见解析
解析
(1)由条件得,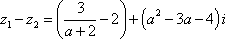
因为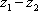
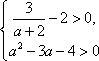
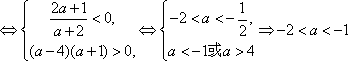
(2)因为虚数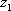
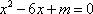
所以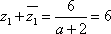
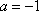
把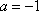
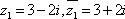
所以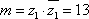
知识点
题干
正确答案
解析
解析
知识点
设



正确答案
解析


因此

又

因此,
知识点
i是虚数单位,复数
正确答案
解析
∵复数


可得 复数


故选C。
知识点
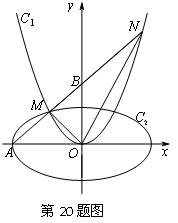
如图,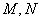
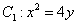
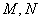
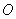
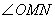
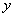
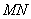
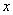
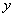
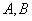
(1)求实数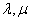
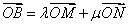
(2)若中心在原点,焦点在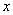
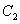
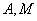
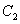
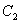
正确答案
见解析。
解析
(1)设
由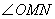
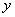
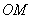
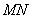
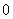
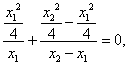

由点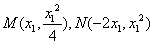
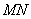
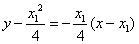
分别在其中令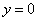
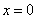
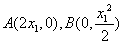
将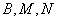
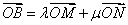
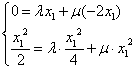
即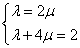
所以
(2) 设椭圆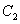
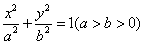
将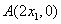
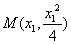
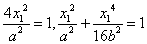
解得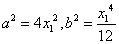
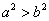
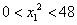
椭圆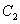
(或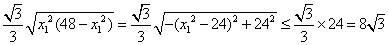
当且仅当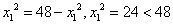
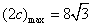
此时椭圆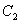
知识点
已知复数



正确答案
-1
解析





知识点
已知函数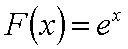
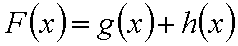
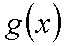
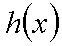
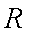
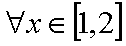
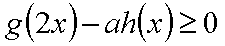
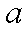
正确答案
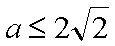
解析
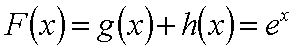
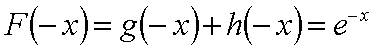
即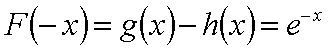
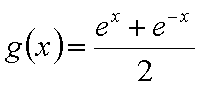
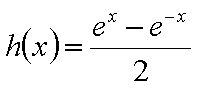
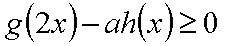
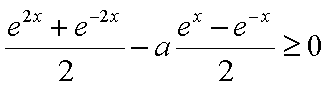
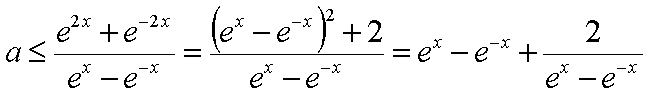
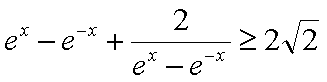
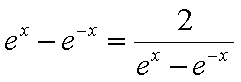
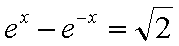
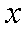
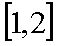
知识点
扫码查看完整答案与解析