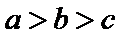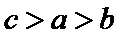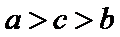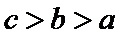- 对数值大小的比较
- 共17题
1
题型：
单选题
|
8.若
A
B
C
D
正确答案
C
知识点
指数函数单调性的应用对数值大小的比较
1
题型：
单选题
|
2．
正确答案
B
解析
解析已在路上飞奔，马上就到！
知识点
指数函数单调性的应用对数值大小的比较
1
题型：
单选题
|
4．已知
①
②
③
④
其中正确的是（ ）
正确答案
D
解析
解析已在路上飞奔，马上就到！
知识点
命题的真假判断与应用对数值大小的比较不等式的性质利用基本不等式求最值
1
题型：
单选题
|
6．设
A
B
C
D
正确答案
C
解析
由对数的图象可知
考查方向
本题主要考查了函数值大小的比较，常见比较大小的方法有作差法、作商法、单调性法、中间值法、图象法等；
解题思路
由于三个对数的底数不同，故可以考虑中间值法和图象法；
易错点
本题易在思路的寻找上迷失。
知识点
对数值大小的比较
1
题型：简答题
|
12.若
正确答案
解析
a和b做比较，a<b,a和c做比较c<a，所以填
考查方向
本题主要指数和对数的大小比较
解题思路
分别比较大小
易错点
找不到中间值（桥梁）
知识点
指数函数单调性的应用对数值大小的比较
1
题型：
单选题
|
10.已知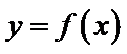
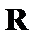
且当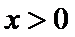
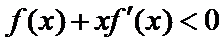
若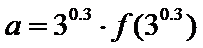
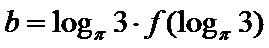
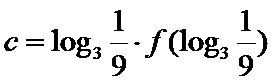
则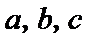
A
B
C
D
正确答案
D
解析
试题分析：令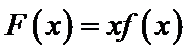
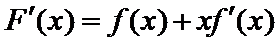
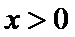
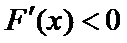
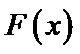
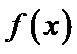
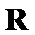
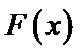
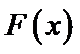
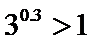
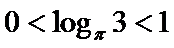
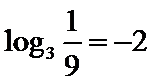
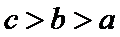
考查方向
本题主要考查了函数的奇偶性、导数的应用等知识点，为高考必考题，在近几年的各省高考题出现的频率较高，常与函数的性质、导数的应用等知识点交汇命题。
解题思路
构造函数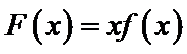
易错点
不能构造出新函数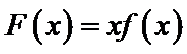
知识点
函数奇偶性的性质指数幂的运算对数值大小的比较导数的运算
下一知识点 : 对数函数的图像与性质
扫码查看完整答案与解析