- 圆的标准方程
- 共116题
已知圆
(1)设点

(2)如图,



正确答案
见解析
解析
(1)由题意知所求的切线斜率存在,设其方程为

由


从而所求的切线方程为

(2)
∴NP为AM的垂直平分线,∴|NA|=|NM|。…………………………………8分又
∴动点N的轨迹是以点C(-1,0),A(1,0)为焦点的椭圆.…………………12分
且椭圆长轴长为
∴点N的轨迹是方程为
知识点
如图所示,点




正确答案
解析
略
知识点
已知圆C与两圆






(1)求圆C的圆心轨迹L的方程;
(2)求满足条件

(3)试探究轨迹Q上是否存在点

正确答案
见解析。
解析
(1)两圆半径都为1,两圆心分别为









(2)因为








(3)由(2)得







因为点B在
故
所以切线与两坐标轴围成的三角形的面积为
设


当



所以点B的坐标为

知识点
从圆
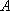
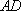
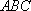
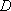
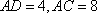


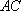
正确答案
4
解析
由切割线定理: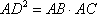
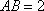
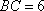

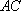

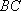
知识点
已知圆C的方程为


正确答案
解析
圆C的方程可化为








知识点
扫码查看完整答案与解析