热门试卷

X 查看更多试卷

题型：单选题

单选题 · 5 分

以抛物线的焦点为圆心,且过坐标原点的圆的方程为( )

正确答案

解析

因为已知抛物线的焦点坐标为（1，0），即所求圆的圆心，又圆过原点，所以圆的半径为，故所求圆的方程为，即

知识点

圆的一般方程抛物线的标准方程和几何性质

题型：单选题

单选题 · 5 分

已知圆的方程为，那么该圆圆心到直线（为参数）的距离为（）

正确答案

解析

略

知识点

圆的标准方程圆的一般方程

题型：单选题

单选题 · 5 分

已知圆的圆心为抛物线的焦点，且与直线相切，则该圆的方程为（）

正确答案

解析

略。

知识点

圆的一般方程直线与圆的位置关系抛物线的标准方程和几何性质

题型：填空题

填空题 · 5 分

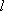
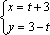
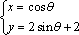
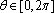
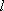
在平面直角坐标系xOy 中，直线的参数方程为（参数t∈R），圆C的参数方程为（参数），则圆C的圆心坐标为_______，圆心到直线的距离为______.

正确答案

（0，2）;

解析

略

知识点

圆的一般方程

题型：单选题

单选题 · 5 分

设有一组圆：. 下列四个命题：

①存在一条定直线与所有的圆均相切； ②存在一条定直线与所有的圆均相交；

③存在一条定直线与所有的圆均不相交； ④所有的圆均不经过原点.

其中真命题的个数为

正确答案

解析

圆的圆心（k-1，3k）在直线y=3（x+1）上运动，因此存在定直线y=3（x+1）与所有的圆均相交；因圆的半径在变化，故①③错，②正确.

对于④：假设存在某个圆经过原点，则（*），下面转化为这个关于k的方程是否有正整数解，可以从k的奇偶性分析：

①若k为奇数，则k-1为偶数，3k为奇数，于是为偶数，为奇数，从而方程（*）的左边为奇数，但方程（*）的右边为偶数，矛盾！

②若k为偶数，则k-1为奇数，3k为偶数，于是为奇数，为偶数，从而方程（*）的左边为奇数，但方程（*）的右边为偶数，矛盾！

综上知，假设不成立，故④正确.

知识点

圆的一般方程

继续学习学习下一知识点

下一知识点 : 轨迹方程

百度题库 > 高考 > 理科数学 > 圆的一般方程

扫码查看完整答案与解析