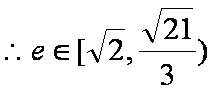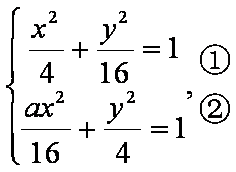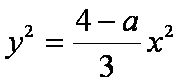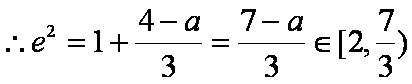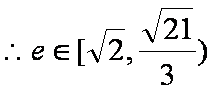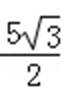圆的标准方程_章节学习

1

题型：简答题

|

简答题 · 13 分

已知动点P到定点的距离和它到定直线的距离的比值为。

（1）求动点P的轨迹的方程；

（2）若过点F的直线与点P的轨迹相交于M，N两点(M，N均在y轴右侧)，点、，设A，B，M，N四点构成的四边形的面积为S，求S的取值范围。

正确答案

见解析。

解析

（1）设动点，则，

化简得。

（2）由（1），轨迹是以为焦点，离心率为的椭圆，如图，连结OM、ON，设直线MN方程为，点，，

联立消去x，得，

则，，

所以，

由于M，N均在y轴右侧，则，，且，

则

， 8分

令，则，则

【或利用求面积S，解法如下：

，则，

。

方法一、，

故面积函数在单调递减，所以，

所以面积S的取值范围是。

方法二、，

因为，则，

所以，

则，即，

所以面积S的取值范围是。

知识点

圆的标准方程

1

题型：简答题

|

简答题 · 10 分

已知圆的极坐标方程为，直线的参数方程为（为参数），点的极坐标为，设直线与圆交于点。

（1）写出圆的直角坐标方程；

（2）求的值.

正确答案

（1）（2）

解析

解析：（1）由，得

， ……………………2分

即

即圆的直角坐标方程为 ……………………4分

（2）由点的极坐标得点直角坐标为……………6分

将代入消去整理得， ……………………8分

设为方程的两个根，则

所以=. ……………………10分

知识点

圆的标准方程

1

题型：简答题

|

简答题 · 10 分

已知在直角坐标系中，直线l过点P，且倾斜角为，以原点O为极点，x轴的正半轴为极轴，建立极坐标系，半径为4的圆C的圆心的极坐标为。

（1）写出直线l的参数方程和圆C的极坐标方程；

（2）试判定直线l和圆C的位置关系。

正确答案

（1）（2）直线和圆C相离

解析

（1）直线的参数方程是，（为参数） …………………2分

圆心C直角坐标为……3分圆C的直角坐标方程为 ……4分

由 …5分得圆C的极坐标方程是. ………6分

（2）圆心的直角坐标是，直线的普通方程是， ………8分

圆心到直线的距离， …………………9分

所以直线和圆C相离. …………………10分

知识点

圆的标准方程

1

题型：填空题

|

填空题 · 5 分

已知焦点在轴上的双曲线的渐近线过椭圆和椭圆（）的交点，则双曲线的离心率的取值范围是

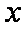
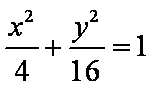
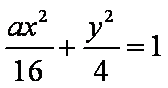
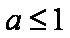
正确答案

解析

①-②可得：

知识点

圆的标准方程

1

题型：单选题

|

单选题 · 5 分

已知球O的半径为R，圆柱内接于球，当内接圆柱的体积最大时，高等于

A

B

C

D

正确答案

A

解析

设球内接圆柱的高为h，则圆柱底面半径

∴

，得

因为只有唯一的零点，所以时取得最大值。故选“A”。

知识点

圆的标准方程

1

题型：单选题

|

单选题 · 5 分

A，B，C，D是同一球面上的四个点，其中△ABC是正三角形，AD⊥平面ABC，AD=2AB=6，则该球的体积为（　　）

A

B48π

C

D

正确答案

A

解析

由题意画出几何体的图形如图，

把A、B、C、D扩展为三棱柱，

上下底面中心连线的中点与A的距离为球的半径，

AD=2AB=6，OE=3，△ABC是正三角形，

所以AE==。

AO==2。

所求球的体积为：=。

故选A。

知识点

圆的标准方程

1

题型：简答题

|

简答题 · 10 分

已知PQ与圆O相切于点A，直线PBC交圆于B、C两点，D是圆上一点，且AB∥CD，DC的延长线交PQ于点Q

（1）求证：

（2）若AQ=2AP，AB=,BP=2，求QD.

正确答案

见解析

解析

解析：（1）因为AB∥CD，所以∠PAB=∠AQC, 又PQ与圆O相切于点A，所以∠PAB=∠ACB,

因为AQ为切线，所以∠QAC=∠CBA,所以△ACB∽△CQA,所以,

所以 ………5分

（2）因为AB∥CD，AQ=2AP，所以,由AB=,BP=2得,PC=6

为圆O的切线

又因为为圆O的切线 ………10分

知识点

圆的标准方程

1

题型：填空题

|

填空题 · 5 分

如图，半径分别为和的圆O1与圆O2外切于T，自圆O2上一点P引圆O1的切线，切点为Q，若PQ=2，则PT= 。

正确答案

PT=

解析

连接PT，延长交圆O于K，连O1O2则O1O2过切点T，由弦切角定理可得，又~

又由切割线定理，得

代入上式，得

知识点

圆的标准方程

1

题型：填空题

|

填空题 · 5 分

已知直角坐标系xoy中，直线l的参数方程为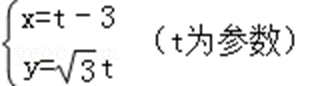，以直角坐标系xOy中的原点O为极点，x轴的非负半轴为极轴，圆C的极坐标方程为ρ2﹣4ρcosθ+3=0，则圆心C到直线l距离为　　。

正确答案

解析

因为直线l的参数方程为。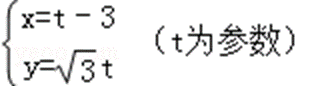

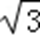
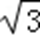
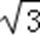
∴ 消去参数t可得直线的普通方程为：y=（x+3）⇒x﹣y+3=0。

又因为圆C的极坐标方程为ρ2﹣4ρcosθ+3=0；

所以：圆的直角坐标方程为：x2+y2﹣4x+3=0，即：（x﹣2）2+y2=1；圆心为（2，0），半径为1。

故圆心到直线的距离为：=。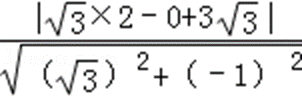

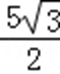
故答案为：。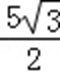

知识点

圆的标准方程

1

题型：简答题

|

简答题 · 12 分

设R，i，j为直角坐标系的单位向量，a=xi+（y+2）j，b=xi+（y－2）j，|a|+|b|=8

（1）求动点M（x，y）的轨迹C的方程

（2）过A（0，3）作直线L与曲线C交于A、B两点，若是否存在直线L使得OAPB为矩形，若存在，求出直线L的方程，若不存在，说明理由

正确答案

见解析

解析

解析：（1）∵a=xi+（y+2）j b=xi+（y+2）j |a|+|b|=8

∴动点M（x，y）是到定点F1（0，－2），F2（0，2）的距离之和8

∴曲线C的轨迹方程为

（2）直线L过N（0，3），若L是y轴，则A，B是椭圆的顶点

∵=+=0，∴P与O重合与OAPB为矩形矛盾

∴直线L的斜率存在，设L：y=kx+3 A（x1，y1）B（x2，y2）

由得（4+3k2）x2+8kx－21=0

∵△=64k2+845（4+3k2）＞0恒成立

∴由韦达定理得x1+x2= x1·x2=

∵=+ ∴OAPB是平行四边形

若存在L，使它为矩形，则⊥ 即·=0 ∴x1·x2+y1·y2=0

即（1+k2）x1x2+3k（x1+x2）+9=0，∴（1+k2）·（－）+3k·（－）+9=0

k2= k=± 所求直线L的方程：y=±x+3。

知识点

圆的标准方程

热门试卷

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点