- 圆的标准方程
- 共116题
已知动点P到定点


(1)求动点P的轨迹的方程;
(2)若过点F的直线与点P的轨迹相交于M,N两点(M,N均在y轴右侧),点

正确答案
见解析。
解析
(1)设动点

化简得
(2)由(1),轨迹是以




联立

则

所以
由于M,N均在y轴右侧,则


则

令

【或利用



方法一、
故面积函数

所以面积S的取值范围是
方法二、
因为

所以
则

所以面积S的取值范围是
知识点
已知球O的半径为R,圆柱内接于球,当内接圆柱的体积最大时,高等于
正确答案
解析
设球内接圆柱的高为h,则圆柱底面半径
∴

因为只有唯一的零点,所以

知识点
A,B,C,D是同一球面上的四个点,其中△ABC是正三角形,AD⊥平面ABC,AD=2AB=6,则该球的体积为( )
正确答案
解析
由题意画出几何体的图形如图,
把A、B、C、D扩展为三棱柱,
上下底面中心连线的中点与A的距离为球的半径,
AD=2AB=6,OE=3,△ABC是正三角形,
所以AE=

AO=

所求球的体积为:

故选A。
知识点
如图,半径分别为


正确答案
PT=
解析
连接PT,延长交圆O于K,连O1O2则O1O2过切点T,由弦切角定理可得

又由切割线定理,得
代入上式,得
知识点
已知直角坐标系xoy中,直线l的参数方程为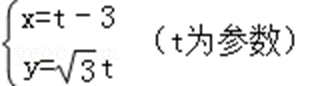
正确答案
解析
因为直线l的参数方程为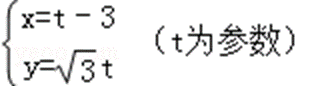
∴ 消去参数t可得直线的普通方程为:y=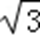
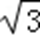
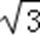
又因为圆C的极坐标方程为ρ2﹣4ρcosθ+3=0;
所以:圆的直角坐标方程为:x2+y2﹣4x+3=0,即:(x﹣2)2+y2=1;圆心为(2,0),半径为1。
故圆心到直线的距离为: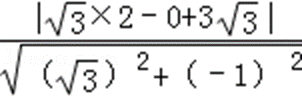
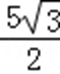
故答案为: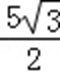
知识点
扫码查看完整答案与解析