- 圆的标准方程
- 共116题
19.已知圆





(1)求曲线
(2)过点







正确答案
(1)依题意,点







(2)由题设直线

将其与抛物线方程联立,消去

设点

故

所以,
解析
解析已在路上飞奔,马上就到!
知识点
8.已知圆C1:(x-2)2+(y-3)2=1,圆C2:(x-3)2+(y-4)2=9,M,N分别是圆C1,C2上的动点,P为x轴上的动点,则|PM|+|PN|的最小值为( ).
正确答案
解析
略
知识点
7.若圆C: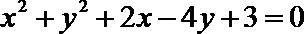

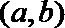
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.已知圆C与圆

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.圆心在直线y=x上,经过原点,且在x轴上截得弦长为2的圆的方程为( )
正确答案
解析
由于圆心在y=x上,所以可设圆的方程为(x-a)2+(y-a)2=r2,将y=0代入得:x2-2ax+2a2=r2∴x1+x2=a,x1•x2=2a2-r2,∴弦长=|x1-x2 |=
知识点
8.已知函数



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13. 过圆








正确答案

解析
解析已在路上飞奔,马上就到!
知识点
15.已知圆

(I)直线






(II)过圆








正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.如图,已知抛物线














(1)求圆

(2)若


(3)过直线




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.已知以点







(Ⅰ)求直线

(Ⅱ)设点



正确答案
解:⑴直线



∴直线

设圆心



又直径


由①②解得
∴圆心
∴圆

(2) 
∴ 当△




又圆心




∴每个圆上都有两个点

所以,共有4个点满足条件
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析



















