- 圆的标准方程
- 共116题
20.已知







(Ⅰ)求
(Ⅱ)一动圆过点


(Ⅲ)过点





正确答案
解:(Ⅰ)

所以AC边所在直线的方程为

由


又
所以

(Ⅱ)设动圆圆心为



所以

故点



从而动圆圆心的轨迹方程

(Ⅲ)

由

故
解析
解析已在路上飞奔,马上就到!
知识点









(Ⅰ)求实数

(Ⅱ)求切线长
(Ⅲ)是否存在以



正确答案
(Ⅰ)连接





化简得实数


(Ⅱ)由






(Ⅲ)


















解析
解析已在路上飞奔,马上就到!
知识点
20.已知点








(1)求动点
(2)已知点





正确答案
解:(1)设
则点
∴
又 
∵ 


∴ 点
(2)假设椭圆



且有
又 

∴ 
得
∴ 
∴ 直线MN的方程为
∴ 椭圆上存在点



解析
解析已在路上飞奔,马上就到!
知识点
7.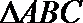
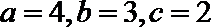
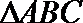
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.过点


正确答案
32
解析
解析已在路上飞奔,马上就到!
知识点
21.如图,在








(

(


正确答案
(



依题可知,由垂径定理可得,


在

即⊙

(


连接




∵

∴

∴


∴

∴
∴
∴

∵

∴直线

解析
解析已在路上飞奔,马上就到!
知识点
4.已知圆


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.设




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.点A、B、C、D均在同一球面上,其中



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.若 △ABC 内接于以O为圆心,1为半径的圆,且

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析