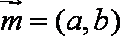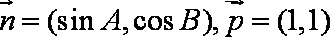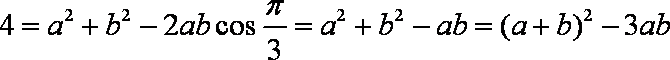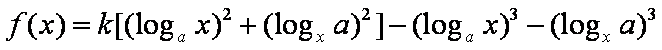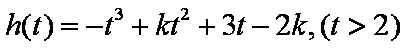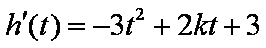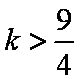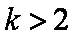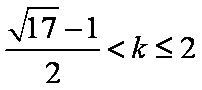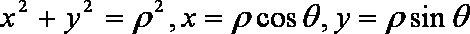- 幂函数的概念、解析式、定义域、值域
- 共682题
已知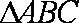
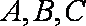
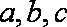
(1)若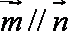
(2)若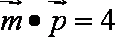
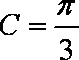
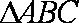
正确答案
见解析。
解析
(1) 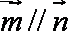
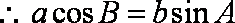
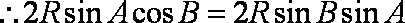
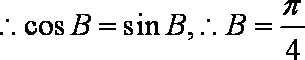
(2)由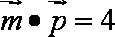
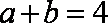
由余弦定理可知:
于是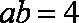
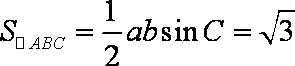
知识点
已知:


(1) 求


(2) 若


正确答案
见解析。
解析
(1)



(2) ∵

∴当



∵
∴
知识点
已知△

(1) 求证:AD的延长线平分
(2) 若




正确答案
见解析。
解析
(1)如图,设F为AD
∵A,B,C,D四点共圆,
∴∠CDF=∠ABC
又AB=AC ∴∠ABC=∠ACB,
且∠ADB=∠ACB, ∴∠ADB=∠CDF,
对顶角∠EDF=∠ADB, 故∠EDF=∠CDF,
即AD的延长线平分∠CDE。
(2)设O为外接圆圆心,连接AO交BC于H,则AH⊥B
连接OC,A由题意∠OAC=∠OCA=150, ∠ACB=750,
∴∠OCH=600。
设圆半径为r,则

知识点
已知函数
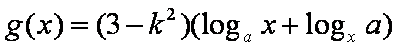
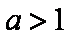
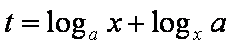
(1)当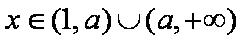
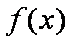
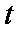
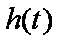
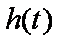
值;
(2)当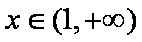
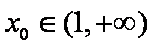
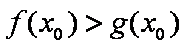
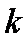
正确答案
见解析。
解析
(1)∵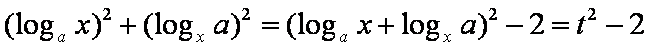
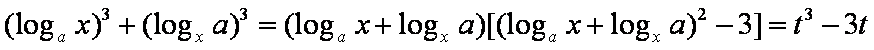
∴
∴
设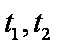
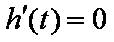
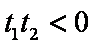
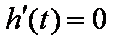
欲使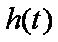
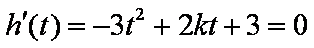
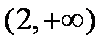
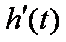
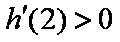
综上:当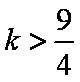
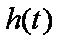
当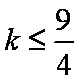
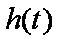
(2)∵存在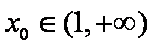
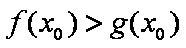
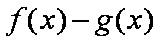
最大值大于0
∵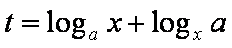
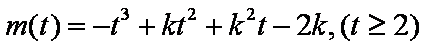
∴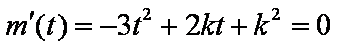
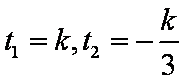
当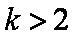
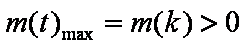
当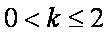
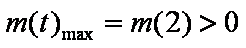
当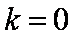
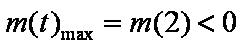
当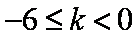
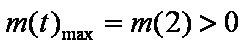

当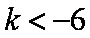
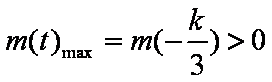
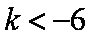
综上得: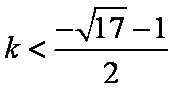
知识点
已知数列
(1) 求数列

(2) 求数列


正确答案
见解析。
解析
(1)由已知

由已知
设等比数列


(2)设数列
则
两式相减得



知识点
点O在



正确答案
5:4
解析
作图如下
作向量

以

平行四边形法则可知:

即2

由已知2


所以

BC是中位线,则OE=2OG=4OH,
则线段OA、OH的长度之比为
从而AH、OH的长度之比为5:1,
所以△ABC与△OBC都以BC为底,对应高之比为5:1,
所以△ABC与△OBC的面
∴三角形ABC的面积与凹四边形ABOC面积之比是5:4
知识点
在




(1)求函数
(2)求
正确答案
见解析。
解析
(1)



应用正弦定理,知


(2)因为

所以,当



知识点
已知椭圆C的中心在坐标原点,右焦点为

(1)求椭圆C的方程;
(2)直线AP与直线
正确答案
见解析
解析
(1)由题意可设椭圆

由题意知

故椭圆

(2)由题意,设直线

则点




由

设点


所以

因为点

当




直线



当


所以直线

点


又因为



综上得,以

知识点
已知极坐标系的极点与直角坐标系的原点重合,极轴与直角坐标系中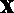
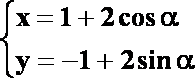
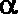
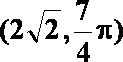
(1)化圆C的参数方程为极坐标方程;
(2)若直线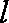
正确答案
见解析
解析
(1)圆C的直角坐标方程为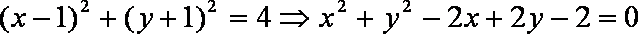
又
∴圆C的极坐标方程为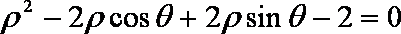
(2)因为点Q的极坐标为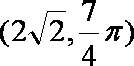
则点Q在圆C内,所以当直线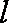
又圆心C(1,-1),∴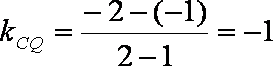
直线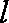
∴直线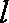
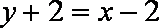
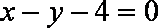
知识点
已知数列



数列。
(1)若



(2)若存在正整数



正确答案
见解析。
解析
(1)依题意,
故
所以
令
则
①


所以
(2)因为
所以

故
又
所以
(ⅰ)当


(ⅱ)当


综上所述,当





知识点
扫码查看完整答案与解析