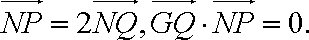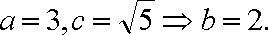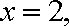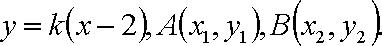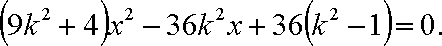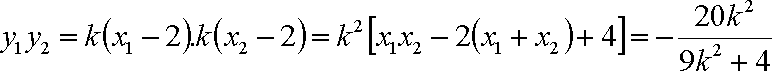- 幂函数的概念、解析式、定义域、值域
- 共682题
己知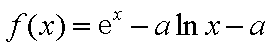
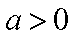
(1)当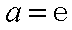
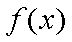
(2)若函数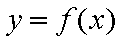
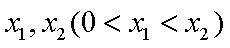
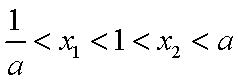
(3)求证: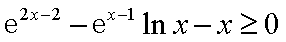
正确答案
见解析。
解析
函数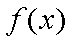
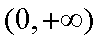
(1)当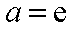
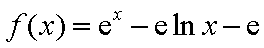
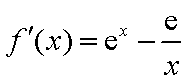
而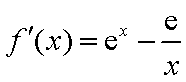
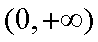
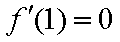
当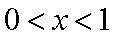
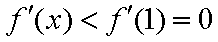
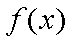
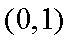
当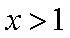
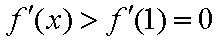
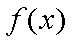
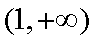
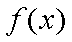
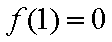
(2)先证明:当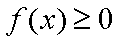
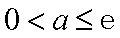
若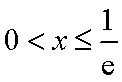
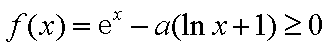
若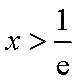
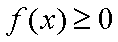
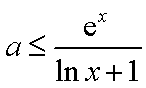
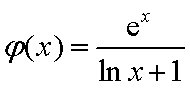
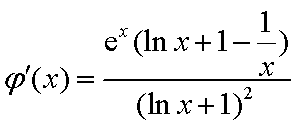
令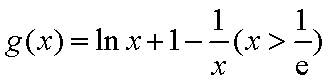
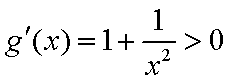
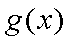
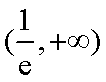
又因为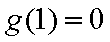
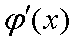
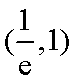
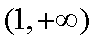
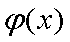
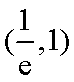
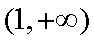
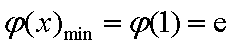
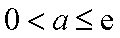
因而函数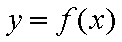

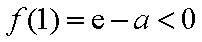
由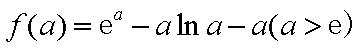
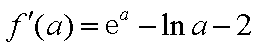
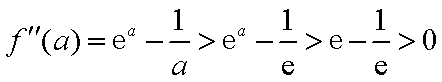
所以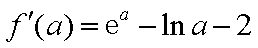
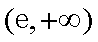
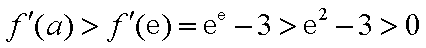
所以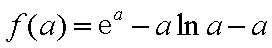
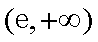
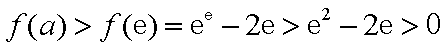
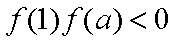
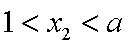
由
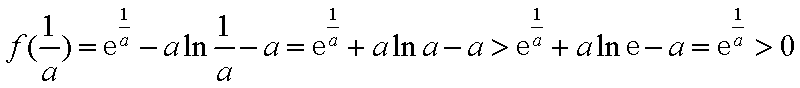
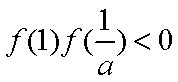
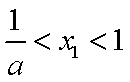
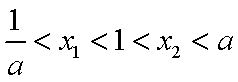
(3)由(2)知当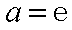
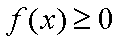
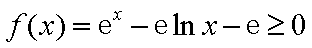
即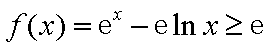
设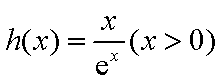
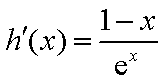
当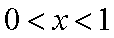
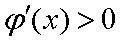
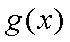
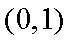
当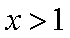
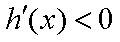
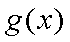
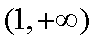
所以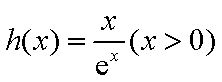
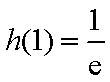
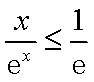
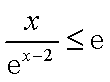
所以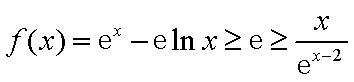
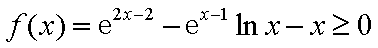
知识点
已知函数

(1)当


(2)当


(3)若


正确答案
见解析
解析
函数


(1)当


所以
所以曲线


即
(2) 当

设

令




令


所以函数


所以函数


所以

于是,当

所以当


(2)问另一方法提示:当

由于



(3)由(2)
设

(1)当


即函数

而












(2)当








故函数



(3)当

当






综上所述
知识点
已知圆


正确答案
a=-2
解析
直线过圆心,由

知识点
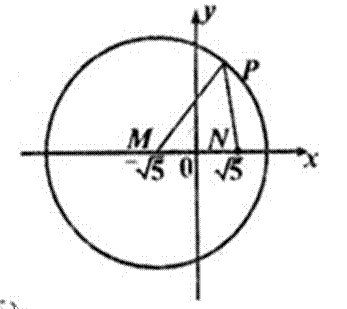
已知圆M: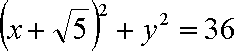
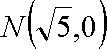
(1)求点G的轨迹C的方程;
(2)过点K(2,0)作直线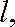
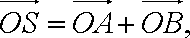
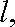
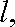
正确答案
见解析。
解析
(1)由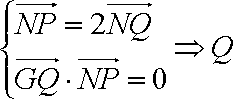
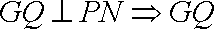
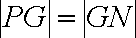
∴>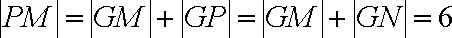

∴点G的轨迹是以M、N为焦点的椭圆,又
∴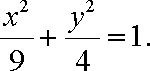
(2)∵.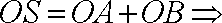
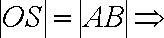

由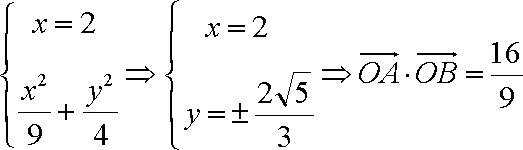

∴1的斜率存在.…………………………………………
设直线1的方程
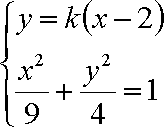
∴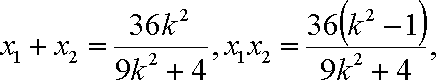
∴
由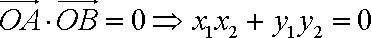
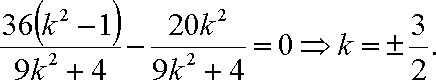
∴存在直线1: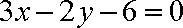
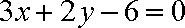
知识点
已知椭圆


(1)求椭圆C的方程;
(2)已知过点



正确答案
见解析。
解析
(1)由题意得
所以椭圆

(2)当直线

当直线


代入

设



设存在符合题意的点
则

设线段


所以
因为


由



所以
由

解得

由

所以
所以存在符合题意的点
知识点
定义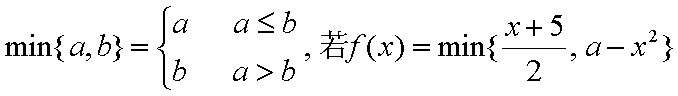
正确答案
4
解析
令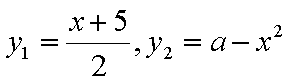
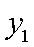
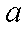
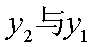
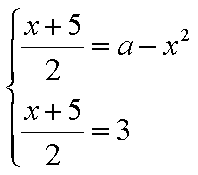
知识点
已知函数
(1)求
(2)求函数

正确答案
见解析。
解析
(1)
则
(2)
则

知识点
下列函数中,周期为

正确答案
解析
知识点
某中学高三文科班学生参加了数学与地理水平测试,学校从测试合格的学生中随机抽取100人
成绩分为优秀、良好、及格三个等级,横向、纵向分别表示地理成绩与数学成绩,例如:表中数学成绩为良好的共有20+18+4=42人。
(1)若在该
(2)若样本中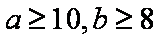
正确答案
见解析。
解析
(1)由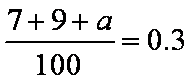
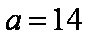
∵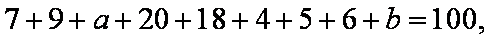
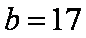
∴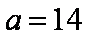
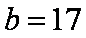
(2)由题意知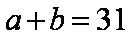
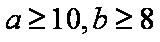
∴满足条件的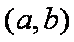
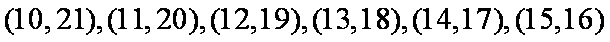
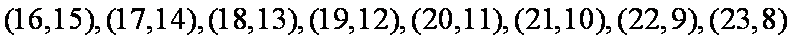
且每组出现的可能性相同,
其中数学成绩优秀的人数比及格的人数少的有:
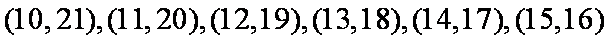
∴数学成绩为优秀的人数比及格的人数少的概率为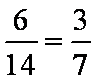
知识点
已知函数

正确答案
解析
由图可知
∴
知识点
扫码查看完整答案与解析