- 幂函数的概念、解析式、定义域、值域
- 共682题
若正项等比数列

正确答案
2
解析
解析:由已知得:








知识点
已知函数
(1)当


(2)若函数



正确答案
见解析
解析
解析:(1)



(2)即
知识点
2012年伦敦奥运会前夕,在海滨城市青岛举行了一场奥运选拔赛,其中甲、乙两名运动员为争取最后一个参赛名额进行了7轮比赛,得分的情况如茎叶图所示(单位:分)。
(1)分别求甲、乙两名运动员比赛成绩的平均分与方差;
(2)若从甲运动员的7轮比赛的得分中任选3个不低于80分且不高于90分的得分,求这3个得分与其平均分的差的绝对值都不超过2的概率.
正确答案
见解析。
解析
(1)


(2)甲运动员的7轮比赛得分中不低于80分且不高于90分的得分共有5个,分别为81,84,85,84,85.
选出的三个得分记为
记“这三个得分与其平均得分的差的绝对值都不超过2”为事件A,事件A包含的基本事件有:(84,85,84),(84,85,85),(84,84,85),(85,84,85),共4种

知识点
在△



(1)求角
(2)求
正确答案
见解析
解析
解:(1)

所以

(2)
因为


故,

知识点
若p是q的必要条件,s是q的充分条件,那么下列推理一定正确的是
正确答案
解析
解:因为p是q的必要条件,s是q的充分条件
所以q⇒p,s⇒q,
所以s⇒p,
所以
知识点
已知

(1)若

(2)若不等式


正确答案
见解析
解析
解:(1)若


当


当


又因为

当



当



故


(2)不等式

设



①当


当


当


从而
故,
②当

令



再令



取


所以,当


这与“
综上所述,
知识点
在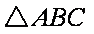
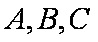
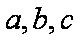

(1)求角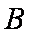
(2)如果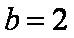
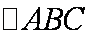
正确答案
见解析
解析
(1)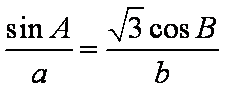
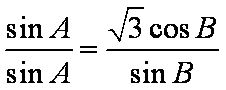
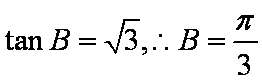
(2)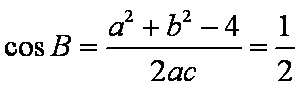
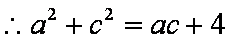
又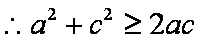
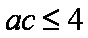
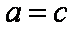
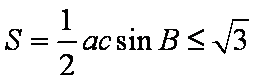
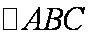
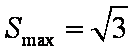
知识点
已知函数
(1)若


(2)若

正确答案
见解析。
解析
(1)函数


由

当









(2)设


由



















即
令
当









解法二:
设
设

当





当

设





当
由



知识点
已知函数
(1)求函数f(x) 的极值点;
(2)若直线 l过点(0,—1),并且与曲线 
(3)设函数


正确答案
见解析。
解析
(1)
而






所以


所以

(2)设切点坐标为

所以切线

又切线

解得
所以直线
(3)






所以


①当



所以

②当1<





③当



所以

综上,当



当

知识点
设
(1)求f (x)的表达式;
(2)如果f (x)是偶函数,求a的值;
(3)当f (x)是偶函数时,讨论函数f (x)在区间(0,+∞)上的单调性,并加以证明
正确答案
见解析
解析
解析:(1)令
∴
(2)∵f (x)是偶函数,∴
即
(3)
∵x1<x2,且

∵0<x1<x2,x1+x2>0,∴
故
∴当x∈(0,+∞)时,f (x)是增函数。
知识点
扫码查看完整答案与解析