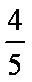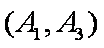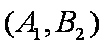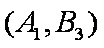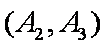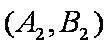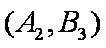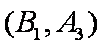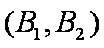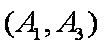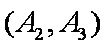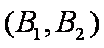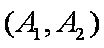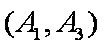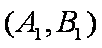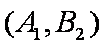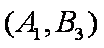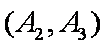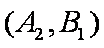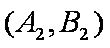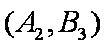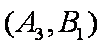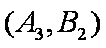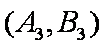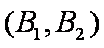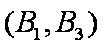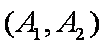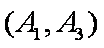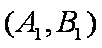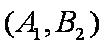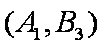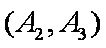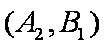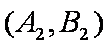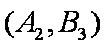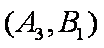- 幂函数的概念、解析式、定义域、值域
- 共682题
函数
正确答案
解析
略
知识点
如图,在四棱锥








(1)证明:

(2)在线段






正确答案
见解析。
解析
(1)∵


又∵



∴

(2)在线段



此时点

且
∵


又∵长方形



又∵


知识点
若


正确答案
解析
略
知识点
已知函数

(1)若函数


(2)若存在


正确答案
见解析·
解析
(1)




此时,



又










(2)存在

即

即存在

令









且


所以只需
知识点
已知向量


(1)求函数


(2)在








正确答案


解析
试题解析:(1)
因为

所以当



(2)由

化简得:


由题意知:




知识点
已知函数
(1)若

(2)设函数

(3)若在区间




正确答案
见解析
解析
(1)当







所以单调减区间为

故

(2)

因为



若




若





所以此时单调减区间为

(3)由第(2)问的解答可知只需在


若




若


若



令
即

设


当










知识点
已知命题

正确答案
解析
略
知识点
设全集
正确答案
解析
略
知识点
甲、乙两个盒子中各有3个球,其中甲盒中有2个黑球1个白球,乙盒中有1个黑球2个白球,所有球之间只有颜色区别。
(1)若从甲、乙两个盒子中各取一个球,求取出的2个球颜色相同的概率;
(2)将这两个盒子中的球混合在一起,从中任取2个, 求取出的2个球中至少有一个黑球的概率。
正确答案
(1)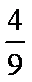
解析
试题解析:将甲盒中的2个黑球1个白球分别记为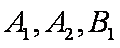
乙盒子中的1个黑球2个白球分别记为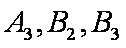
(1)“从甲、乙两个盒子中各取一个球”的基本事件有:
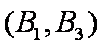
记取出的2个球颜色相同为事件M,则事件M包含的基本事件有: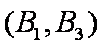
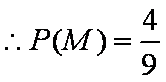
(2)“从6个球中任取两个球”的基本事件有:
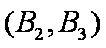
设“取出的2个球中至少有一个黑球”为事件N,则事件N包含的基本事件有: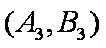
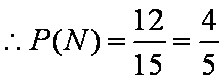
知识点
定义在R上的函数的图像关于直线




正确答案
解析
略
知识点
扫码查看完整答案与解析