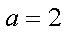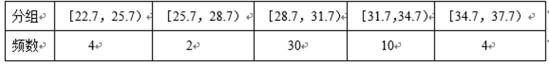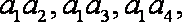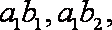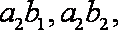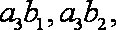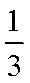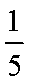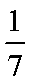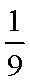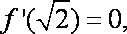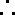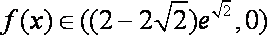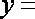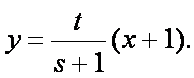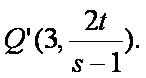- 幂函数的概念、解析式、定义域、值域
- 共682题
已知函数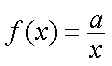
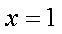
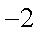
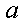
正确答案
2
解析
易得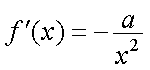
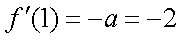
知识点
已知函数
(1)求
(2)求
(3)求

正确答案
见解析。
解析
(1)
所以最小正周期为
(2) 由 
整理,得

(3)当

故当x=0时,

知识点
某省高考数学阅卷点共有400名阅卷老师,为了高效地完成文、理科数学卷的阅卷任务,需将400名阅卷老师分成两组同时展开阅卷工作,一组完成269捆文科卷,另一组完成475捆理科卷,根据历年阅卷经验,文科每捆卷需要一位阅卷老师工作3天完成,理科每捆卷需要一位阅卷老师工作4天完成,(假定每位阅卷老师工作一天的阅卷量相同,每捆卷的份数也相同)
(1)如何安排文、理科阅卷老师的人数,使得全省数学阅卷时间最省?
(2)由于今年理科阅卷任务较重,理科实际每捆卷需要一位阅卷老师工作4.5天完成,在按(1)分配的人数阅卷4天后,阅卷领导小组决定从文科组抽调20名阅卷老师去阅理科卷,试问完成全省数学阅卷任务至少需要多少天?(天数精确到小数点后第3位)
(参考数据:



正确答案
见解析
解析
(1)设文科阅卷人数为

则阅卷时间为
而

答:当文、理科阅卷人数分别是119,281时,全省阅卷时间最省;
(2)文科阅卷时间为:
理科阅卷时间为:
答:全省阅卷时间最短为
知识点
有一座大桥既是交通拥挤地段,又是事故多发地段,为了保证安全,交通部门规定。大桥上的车距d(m)与车速v(km/h)和车长l(m)的关系满足:
(1)写出车距d关于车速v的函数关系式;
(2)应规定怎样的车速,才能使大桥上每小时通过的车辆最多?
正确答案
见解析
解析
(1)因为当


∴
(2)设每小时通过的车辆为

∵
∴




答:当
知识点
从总体中抽取容量为50的样本,数据分组及各组的频数如下:
(1)估计尺寸在[28.7,34.7)的概率;
(2)从样本尺寸在[22.7,28.7)中任选2件,求至少有1个尺寸在[25.7,28.7)的概率.
正确答案
见解析。
解析
(1)尺寸在[28.7,34.7)中共有40个,所以所求的概率为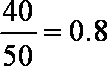
(2)设尺寸在[22.7,25.7)中的产品编号为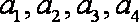
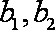
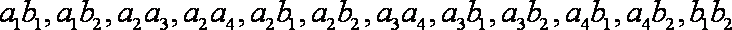
------------------- 7分
其中至少有1个尺寸在[25.7,28..7)中的有:
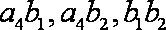
因此所求概率为
知识点
在游乐场,有一种游戏是向一个画满均匀方格的桌面上投硬币,若硬币恰落在任何一个方格内不与方格线重叠,即可获奖,已知硬币的直径为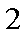
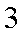
正确答案
解析
考查几何概型,游客获奖的概率为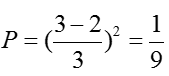
知识点
已知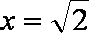
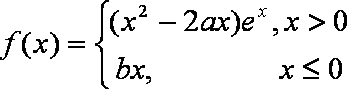
(1)当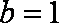
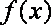
(2)当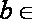
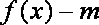
正确答案
见解析。
解析
(1)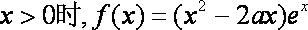
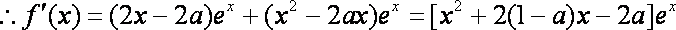
由已知得,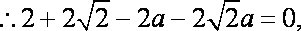
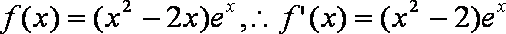
当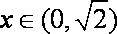
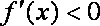
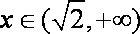
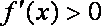
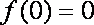
当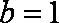
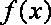
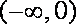
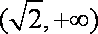
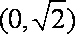
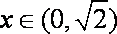
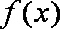
当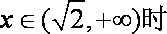
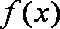
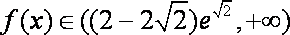
要使函数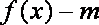
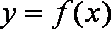
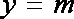
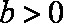
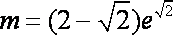
②当b=0时,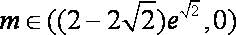
③当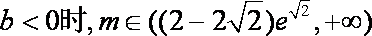
知识点
已知圆O的方程为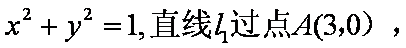
(1)求直线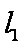
(2)设圆O与x轴交与P,Q两点,M是圆O上异于P,Q的任意一点,过点A且与x轴垂直的直线为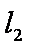
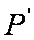
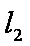
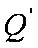
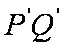
正确答案
见解析
解析
(1)∵直线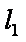
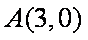

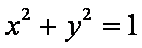
设直线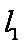
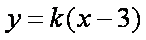
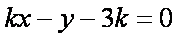
则圆心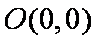
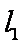
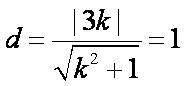

∴直线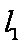
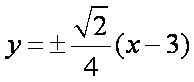
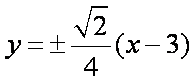
(2)对于圆方程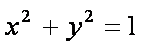
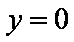
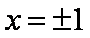
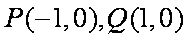
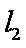
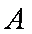
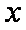
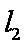
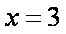
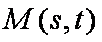
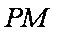
解方程组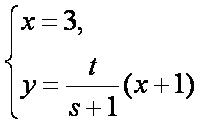
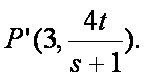
∴以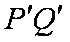
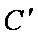

又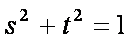
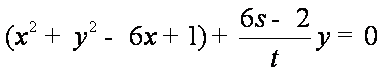
若圆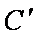
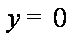
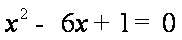
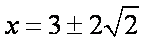
∴圆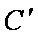
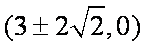
知识点
一铁棒欲通过如图所示的直角走廊,试回答下列问题:
(1)求棒长L关于

(2)求能通过直角走廊的铁棒的长度的最大值。
正确答案
见解析
解析
(1)
如图,
(2)
令


则




所以
所以能够通过这个直角走廊的铁棒的最大长度为4
知识点
已知抛物线



(1)求抛物线

(2)过点






(3)直线










正确答案
见解析
解析
(1)由抛物线





同理由椭圆





(2)设直线


联立方程组



由
整理得:

(3)设
由



由①+②+③得
∴

知识点
扫码查看完整答案与解析