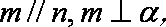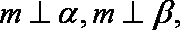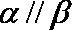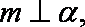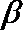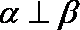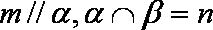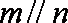- 幂函数的概念、解析式、定义域、值域
- 共682题
已知椭圆E:

(1)求椭圆E的方程;
(2)设直线PF2的倾斜角为α,直线PF1的倾斜角为β,当β-α=时,证明:点
P在一定圆上。
正确答案
见解析
解析
(1)圆


故


(2)设点


因为



所以

因为

因为
所以
化简得

知识点
在数列




(1) 若

(2) 若对任意的



① 求证:
② 若



正确答案
见解析
解析
解: (1)因为


所以
(注: 讲评时可说明, 此时数列
(2)①因为

而

得


所以
②因为



(ⅰ)当






所以

(ⅱ)当





所以
则


综上所述,
知识点
已知函数

(1)求实数
(2)若



(3)当

正确答案
见解析
解析
解析:(1)
令
故


(2)当

令



由于



则









(3)要证
即证 

令
又





知识点
已知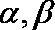
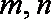
正确答案
解析
选项D中,直线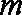
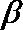
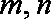
知识点
调查某初中1000名学生的肥胖情况,得下表:
已知从这批学生中随机抽取1名学生,抽到偏瘦男生的概率为0.15.
(1)求
(2)若用分层抽样的方法,从这批学生中随机抽取50名,问应在肥胖学生中抽多少名?
(3)已知

正确答案
见解析。
解析
(1)由题意可知,

(2)由题意可知,肥胖学生人数为
设应在肥胖学生中抽取


所以应在肥胖学生中抽20名. ……………7分
(3)由题意可知, 



设事件



即肥胖学生中女生少于男生的概率为
知识点
已知函数




正确答案
解析
当






知识点
已知函数






(1)求
(2)将函数






正确答案
见解析。
解析
(1)
-------------------------------------------3分
由题意知,最小正周期


∴
(2)将




令







∴

知识点
随着机构改革开作的深入进行,各单位要减员增效,有一家公司现有职员







正确答案
见解析
解析
设裁员x人,可获得的经济效益为y万元,则
依题意
(1)当
(2)当
答:当 

当

知识点
函数




正确答案
解析
令










知识点
已知α为锐角,

正确答案
解析
由




知识点
扫码查看完整答案与解析