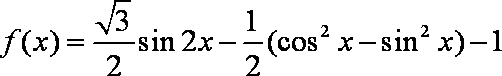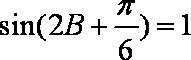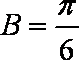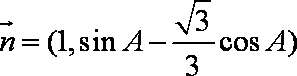- 幂函数的概念、解析式、定义域、值域
- 共682题
直线




正确答案
解析
直线方程为
知识点
已知函数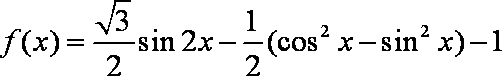
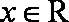
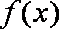
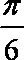
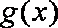
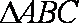
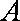
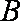
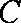
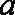
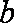
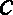
(1)若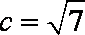
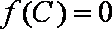
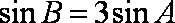
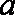
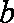
(2)若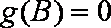
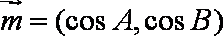
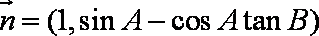
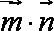
正确答案
见解析。
解析
(1)
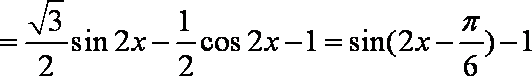
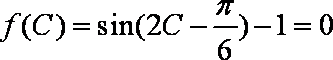
因为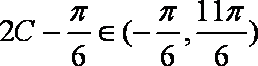
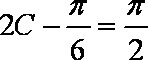
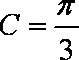

由余弦定理知: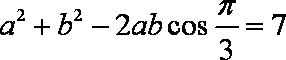
因为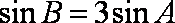
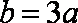
解得: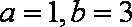
(2)由条件知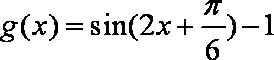
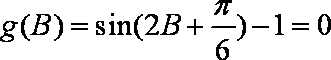
所以
因为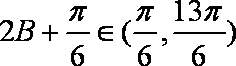
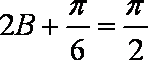
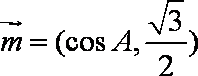
于是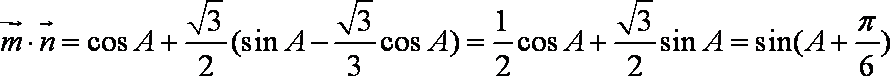
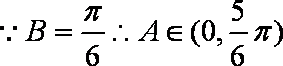
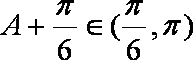
∴ 
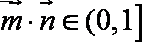
知识点
已知函数
(1)求函数
(2)当


正确答案
见解析。
解析
(1)

令
得
∴

(2)由

所以当


知识点
已知函数
(1) 求函数
(2) 求证:当
(3) 如果

正确答案
见解析。
解析
(1)



令


∴当



(2)证明:


当



∴



(3)证明:∵


∴当



∴
由⑵的结论知


∵

又

知识点
已知数列






(1)求数列
(2)若


正确答案
见解析。
解析
(1)由



(2)数列


从而
∴
∴
=
从而.
知识点
在游乐场,有一种游戏是向一个画满均匀方格的桌面上投硬币,若硬币恰落在任何一个方格内不与方格线重叠,即可获奖,已知硬币的直径为


正确答案
解析
考查几何概型,游客获奖的概率为
知识点
已知
正确答案
解析
因为



知识点
设函数y=f(x)满足对任意的x∈R,f(x)≥0且f2(x+1)+f2(x)=9.已知当x∈[0,1]时,有f(x)=2﹣|4x﹣2|,则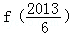
正确答案
解析
∵f2(x+1)+f2(x)=9,即 f2(x+1)=9﹣f2(x),
∴f2(x+2)=9﹣f2(x+1),化简可得 f2(x+2)=9﹣[9﹣f2(x)]=f2(x)。
再由 函数y=f(x)满足对任意的x∈R,f(x)≥0,可得 f(x+2)=f(x),故函数是周期为2的周期函数。
∴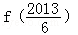
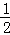
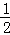
又 f2(﹣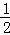
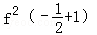
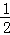
再由当x∈[0,1]时,有f(x)=2﹣|4x﹣2|,可得f(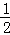
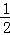
故 f2(﹣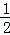
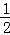
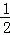
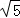
故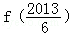
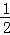
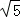
知识点
已知
(1)当

(2)若函数


(2)当

正确答案
见解析
解析
(1)当


当


则函数


(2)


令


(3)令








知识点
已知向量
(1)求函数
(2)在△ABC中,a,b,c分别是角A,B,C的对边,A为锐角,若

正确答案
见解析。
解析
(1)由题意得

令
解得:


所以函数



(2)由
化简得:
又因为

由题意知:

又
故所求边

知识点
扫码查看完整答案与解析