圆锥曲线与方程_章节学习

1

题型：填空题

|

填空题 · 20 分

请你谈一谈对“不同生产方式以及生产工艺中，生产物流管理所采用的方法和手段是不同的。”这句话的理解。

正确答案

测试

1

题型：填空题

|

填空题 · 20 分

请你谈一谈对“不同生产方式以及生产工艺中，生产物流管理所采用的方法和手段是不同的。”这句话的理解。

正确答案

测试

1

题型：简答题

|

简答题 · 13 分

设矩阵（其中＞0，＞0）。

（1）若=2，=3，求矩阵的逆矩阵；

（2）若曲线：在矩阵所对应的线性变换作用下得到曲线：，求，的值。

正确答案

（1）

解析

（1）设矩阵M的逆矩阵，则

又，所以，

∴

故所求的逆矩阵

（2）设曲线C上任意一点，

它在矩阵M所对应的线性变换作用下得到点，

则

又点在曲线上， ∴.

则为曲线C的方程，

又已知曲线C的方程为

又

知识点

椭圆的定义及标准方程

1

题型：简答题

|

简答题 · 12 分

如图，设Ｐ是圆上的动点，点Ｄ是Ｐ在轴上投影，Ｍ为PD上一点，且。

（1）当P在圆上运动时，求点M的轨迹C的方程；

（2）求过点（3，0）且斜率为的直线被C所截线段的长度。

正确答案

（1）（2）

解析

（1）设点M的坐标是，P的坐标是，

因为点Ｄ是Ｐ在轴上投影，

Ｍ为PD上一点，且，所以，且，

∵P在圆上，∴，整理得，

即C的方程是。

（2）过点（3，0）且斜率为的直线方程是，

设此直线与C的交点为，，

将直线方程代入C的方程得：

，化简得，∴，，

所以线段AB的长度是

，即所截线段的长度是。

知识点

椭圆的定义及标准方程

1

题型：填空题

|

填空题 · 5 分

若椭圆的焦点在x轴上，过点作圆的切线，切点分别为A，B，直线AB恰好经过椭圆的右焦点和上顶点，则椭圆方程是 .

正确答案

解析

设过点（1，）的直线方程为：当斜率存在时，，

根据直线与圆相切，圆心（0,0）到直线的距离等于半径1可以得到k=,直线与圆方程的联立可以得到切点的坐标（），当斜率不存在时，直线方程为：x=1，根据两点A：（1,0），B：（）可以得到直线：2x+y-2=0,则与y轴的交点即为上顶点坐标（2,0），与x轴的交点即为焦点，根据公式，即椭圆方程为：

知识点

椭圆的定义及标准方程

1

题型：填空题

|

填空题 · 4 分

若抛物线的焦点与椭圆的右焦点重合，则该抛物线的准线方程为 .

正确答案

解析

椭圆右焦点为，即抛物线焦点，所以准线方程

知识点

椭圆的定义及标准方程椭圆的几何性质抛物线的定义及应用

1

题型：简答题

|

简答题 · 14 分

已知椭圆，过点作圆的切线交椭圆于，两点。

（1）求椭圆的焦点坐标和离心率；

（2）将表示为的函数，并求的最大值。

正确答案

（1）离心率为

（2）|AB|的最大值为2.

解析

（1）由已知得∴

∴椭圆G的焦点坐标为,离心率为

（2）由题意知，.

当时，切线l的方程，点A、B的坐标分别为

此时

当m=－1时，同理可得

当时，设切线l的方程为

由

设A、B两点的坐标分别为，则

又由l与圆

所以

由于当时，

所以.

因为

且当时，|AB|=2，所以|AB|的最大值为2.

知识点

椭圆的定义及标准方程

1

题型：简答题

|

简答题 · 12 分

乒乓球比赛规则规定：一局比赛，双方比分在10平前，一方连续发球2次后，对方再连续发球2次，依次轮换，每次发球，胜方得1分，负方得0分。设在甲、乙的比赛中，每次发球，发球方得1分的概率为，各次发球的胜负结果相互独立，。甲、乙的一局比赛中，甲先发球。

（1）求开始第4次发球时，甲、乙的比分为1比2的概率；

（2）表示开始第4次发球时乙的得分，求的期望。

正确答案

见解析。

解析

：记为事件“第i次发球，甲胜”，i=1,2,3，则。

（1）事件“开始第次发球时，甲、乙的比分为比”为，由互斥事件有一个发生的概率加法公式得

。

即开始第次发球时，甲、乙的比分为比的概率为0.352

（2）由题意。

；

=0.408；

；

所以

知识点

椭圆的定义及标准方程

1

题型：单选题

|

单选题 · 5 分

如图，某飞行器在4千米高空水平飞行，从距着陆点的水平距离10千米处下降，已知下降飞行轨迹为某三次函数图像的一部分，则函数的解析式为（）

A

B

C

D

正确答案

A

解析

知识点

椭圆的定义及标准方程

1

题型：简答题

|

简答题 · 12 分

如图，四棱锥中，为矩形，平面平面.

（1）求证：

（2）若问为何值时，四棱锥的体积最大？并求此时平面与平面夹角的余弦值。

正确答案

见解析。

解析

（1）∵在四棱锥P﹣ABCD中，ABCD为矩形，∴AB⊥AD，

又∵平面PAD⊥平面ABCD，平面PAD∩平面ABCD=AD，

∴AB⊥面PAD，∴AB⊥PD。

（2）过P做PO⊥AD，∴PO⊥平面ABCD，

作OM⊥BC，连接PM

∴PM⊥BC，

∵∠BPC=90°，PB=，PC=2，

∴BC=，PM==，BM=，

设AB=x，∴OM=x∴PO=，

∴VP﹣ABCD=×x××=

当，即x=，VP﹣ABCD=，

建立空间直角坐标系O﹣AMP，如图所示，

则P（0，0，），D（﹣，0，0），C（﹣，，0），M（0，，0），B（，，0）

面PBC的法向量为=（0，1，1），面DPC的法向量为=（1，0，﹣2）

∴cosθ===﹣。

知识点

椭圆的定义及标准方程

1

题型：填空题

|

填空题 · 20 分

请你谈一谈对“不同生产方式以及生产工艺中，生产物流管理所采用的方法和手段是不同的。”这句话的理解。

正确答案

测试

1

题型：填空题

|

填空题 · 20 分

请你谈一谈对“不同生产方式以及生产工艺中，生产物流管理所采用的方法和手段是不同的。”这句话的理解。

正确答案

测试

1

题型：填空题

|

填空题 · 20 分

请你谈一谈对“不同生产方式以及生产工艺中，生产物流管理所采用的方法和手段是不同的。”这句话的理解。

正确答案

测试

1

题型：单选题

|

单选题 · 5 分

阅读如图所示的程序框图，运行相应的程序，输出的S的值等于（　　）

A18

B20

C21

D40

正确答案

B

解析

【考查点】循环结构。

计算题；算法和程序框图。

算法的功能是求S=21+22+…+2n+1+2+…+n的值，计算满足条件的S值，可得答案。

由程序框图知：算法的功能是求S=21+22+…+2n+1+2+…+n的值，

∵S=21+22+1+2=2+4+1+2=9＜15，S=21+22+23+1+2+3=2+4+8+1+2+3=20≥15。

∴输出S=20。

知识点

椭圆的定义及标准方程

1

题型：单选题

|

单选题 · 5 分

复数z=（3﹣2i）i的共轭复数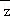等于（　　）

A﹣2﹣3i

B﹣2+3i

C2﹣3i

D2+3i

正确答案

C

解析

数系的扩充和复数。

直接由复数代数形式的乘法运算化简z，则其共轭可求。

∵z=（3﹣2i）i=2+3i，

∴。

知识点

椭圆的定义及标准方程

热门试卷

正确答案

正确答案

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

正确答案

正确答案

正确答案

解析

知识点

正确答案

解析

知识点