- 计数原理
- 共551题
如果在一周内(周一至周日)安排三所学校的学生参观某展览馆,每天最多只安排一所学校,要求甲学校连续参观两天,其余学校均只参观一天,那么不同的安排方法有()种.
正确答案
120
解析
略
知识点
根据以往统计资料,某地车主购买甲种保险的概率为0.5,购买乙种保险但不购买甲种保险的概率为0.3,设各车主购买保险相互独立。
(1)求该地1为车主至少购买甲、乙两种保险中的1种的概率;
(2)X表示该地的100为车主中,甲、乙两种保险都不购买的车主数,求X的期望。
正确答案
见解析。
解析
设该车主购买乙种保险的概率为p,由题意知: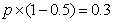
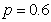
(1)设所求概率为P1,则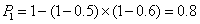
故该地1位车主至少购买甲、乙两种保险中的1种的概率为0.8。
(2)对每位车主甲、乙两种保险都不购买的概率为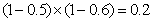
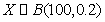
所以X的期望是20人。
知识点
5名志愿者到3个不同的地方参加义务植树,则每个地方至少有一名志愿者的方案共有________种。
正确答案
150
解析
略
知识点
从甲、乙等5个人中选出3人排成一列,则甲不在排头的排法种数是()
正确答案
解析
略
知识点
已知函数
(1)证明:

(2)若关于x的不等式

(3)已知正数a满足:存在



正确答案
见解析。
解析
本小题主要考查初等函数的基本性质、导数的应用等基础知识,考查综合运用数学思想
方法分析与解决问题的能力。
(1)



(2)由题意,
∵



令


∵

∴
(3)




令
∵



∵存在


∵
设
当


当


因此
∴当


当


当


知识点
某公园设有自行车租车点, 租车的收费标准是每小时2元(不足1小时的部分按1小时计算).甲、乙两人各租一辆自行车,若甲、乙不超过一小时还车的概率分别为

(1)求甲、乙两人所付租车费用相同的概率;
(2)设甲、乙两人所付的租车费用之和为随机变量


正确答案
见解析
解析
(1)甲、乙两人所付费用相同即为


都


都付

都付

故所付费用相同的概率为
(2)依题意











故

所求数学期望
知识点
某水域一艘装载浓硫酸的货船发生侧翻,导致浓硫酸泄漏,对河水造成了污染.为减少对环境的影响,环保部门迅速反应,及时向污染河道投入固体碱,




(1)如果只投放1个单位的固体碱,则能够维持有效的抑制作用的时间有多长?
(2)第一次投放1单位固体碱后,当污染河道水中的碱浓度减少到


正确答案
见解析。
解析
(1)由题意知
解得

能够维持有效的抑制作用的时间:
(2)由(1)知,

当




当
当


当

所以
当



当且仅当

当
当


当



又


答:第一次投放1单位固体碱能够维持有效的抑制作用的时间为3小时;第一次投放

知识点
从5名学生中任选4名分别参加数学、物理、化学、生物四科竞赛,且每科竞赛只有1人参加,若甲不参加生物竞赛,则不同的选择方案共有()种。
正确答案
96
解析
略
知识点
在

正确答案
84
解析
略
知识点
若
正确答案
80
解析
二项式展开式的通项公式为 Tr+1=

故答案为 80。
知识点

正确答案
解析
略
知识点
某小区有排成一排的


正确答案
解析
略
知识点
如果在一周内(周一至周日)安排三所学校的学生参观某展览馆,每天最多只安排一所学校,要求甲学校的学生连续参观两天,其余学校的学生均只参观一天,则不同的安排方法共有
正确答案
解析
先安排甲学校的参观时间,一周内两天连排的方法共有6种,甲任选一种为


知识点
某人从标有1、2、3、4的四张卡片中任意抽取两张.约定如下:如果出现两个偶数或两个奇数,就将两数相加的和记为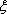

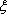
正确答案
解析
略
知识点
一组数据9.8, 9.9, 10,a, 10.2的平均数为10,则该组数据的方差为 .
正确答案
0.02
解析
由已知先求得
知识点
扫码查看完整答案与解析