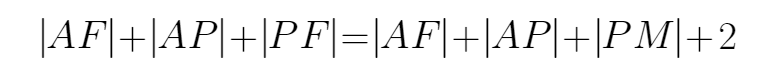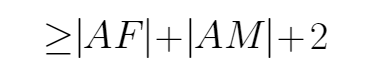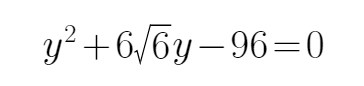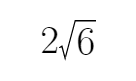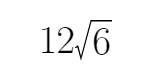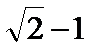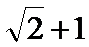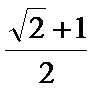- 圆锥曲线与方程
- 共2626题
前间壁心肌梗死特征性心电图改变,见于
A.V3、V4、V5
B.V1、V2、V3、V4、V5
C.V1、V2、V3
D.V5、I、aVL
E.Ⅱ、Ⅲ、aVF
正确答案
C
解析
暂无解析
16.已知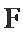
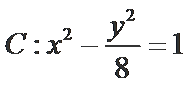
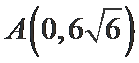
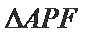
正确答案
解析
由题意可知,设M为左焦点,所以三角形APF的周长为
所以直线AM的方程为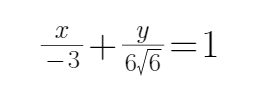
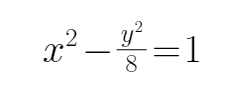
所以P的纵坐标为
所以三角形APF周长最小时,该三角形的面积为:
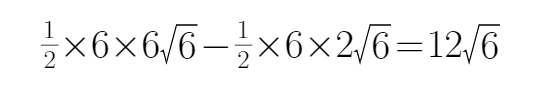
考查方向
双曲线的性质,双曲线的图像的特征
解题思路
利用双曲线的定义,确定APE周长最小时,求三角形的面积
易错点
对双曲线的性质和特征掌握不好
知识点
乙在一次滑坡灾难中与唯一的11岁女儿丙失散,三个月后,乙的朋友甲在街上看到丙,惊喜万分,就将丙带回家,并马上致电已经搬到另一个城市的乙,乙答应连夜赶来,但因公务缠身,第三天才到。在这期间,甲带丙到商场买用品,途中丙口渴,甲让丙站在原处,自己到对面买水,回来发现,丙再次失踪。对于丙的再次失踪,下列表述正确的是( )。
A.甲应承担主要责任,乙承担次要责任
B.乙具有重大过失,应责任自负
C.甲可以免责
D.甲应根据过失相抵承担相应的责任
正确答案
C
解析
[考点] 无因管理中的侵权责任 [解析] 无因管理作为一种债的发生根据,是指没有法定的或者约定的义务,为避免他人利益受损失而进行管理或者服务的法律事实。因为无因管理行为的成立,管理人须承担一定的义务:一是适当管理的义务。即不违反本人的意思,以有利于本人的方法为适当管理的义务。管理人未尽适当管理义务的,发生债务不履行的法律后果,应当依法承担相应的民事责任。但是,为了鼓励无因管理行为,一般认为管理人在管理事务过程中,只有因故意或重大过失而侵害本人的人身或财产权利时,才构成侵权行为。二是通知义务。三是报告与计算的义务。 在本题中,甲在街上看到乙失散的女儿丙,就将丙带回家,属于无法定的或约定的义务,为避免他人利益受损失而进行管理或者服务,成立无因管理行为。甲“马卜致电已经搬到另一个城市的乙”,是履行通知义务;在乙赶来的期间内, “甲带丙到商场买用品,途中丙口渴,甲让丙站在原处,自己到对面买水”,是履行适当管理的义务。 正如上文分析,无因管理人只有在主观上具有故意或重大过失时才承担侵权责任。在本题中,乙的女儿已经11岁,属于限制民事行为能力人,甲在无法分身的情况下,嘱咐丙“站在原处,自己到对面买水”,并没有故意或重大过失,其对丙的再次失踪,不应该承担责任。 因此,选项A“甲应承担主要责任,乙承担次要责任”和选项D“甲应根据过失相抵承担相应的责任”都是错误的。 我们一般依据注意义务的大小对过失分为三类:一是重大过失,即违反普通人的注意义务,二是具体轻过失,指行为人违反应与处理自己事务相同的义务;三是抽象轻过失,即违反善良管理人的注意义务。通过上文分析,甲让丙站在原处,自己到对面买水的行为并没有违反普通人的注意义务。所以选项C的表述是可以成立的, 选项B“乙具有重大过失,应责任自负”与题意不符,乙承担不利法律后果与其主观上的过错没有必然关系,不应当选。
10.已知直线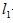
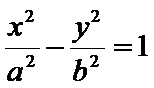
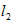
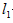

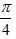
正确答案
解析
:
考查方向
解题思路
由双曲线通径公式找到两直线构成的三角形,在利用三角形性质构成等式,利用a,b,c关系解得离心率
易错点
本题易错于忽略双曲线的通经,通过通径与直线组成三角形关系求离心率
知识点
某小区的设备系统共有设备82台套,在设备检查中发现其中有2台套已报废,有4台套陈旧老化已不能工作,另有3台套发生运行故障,正在维修中,问该小区设备系统的设备完好率是多少( )
A.92.68%
B.89.02%
C.97.56%
D.96.34%
正确答案
B
解析
暂无解析
金融市场的功能可以从微观和宏观两个方面来考察,下列属于宏观经济功能的是( )。
A.交易功能
B.反映功能
C.集聚功能
D.调节功能
E.资源配置功能
正确答案
B,D,E
解析
[解析] 金融市场的宏观经济功能是:资源配置功能、调节功能和反映功能。选项AC属于金融市场的微观经济功能。
14.若抛物线

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.在平面直角坐标系




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.将离心率为






正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.已知A,B为双曲线E的左,右顶点,点M在E上,∆ABM为等腰三角形,且顶角为120°,则E的离心率为( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.双曲线

正确答案
解析
双曲线

双曲线

可得:


即




故选A.
考查方向
解题思路
先根据双曲线方程求得双曲线的渐近线,进而利用圆心到渐近线的距离为圆的半径求得a和b的关系,进而利用
易错点
直线与圆相切,圆心到直线的距离等于半径.
知识点
正确答案
知识点
正确答案
知识点
正确答案
知识点
20. 如图,双曲线






(1)当直线



正确答案
2
右支上不存在
解析
双曲线的焦点在















当直线











设直线























考查方向
解题思路
先求出焦点坐标以及直线


写出直线




设直线




则








易错点
计算要仔细。
①计算要准确仔细②注意计算技巧
知识点
扫码查看完整答案与解析