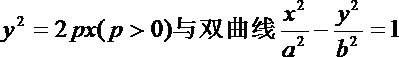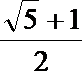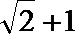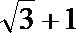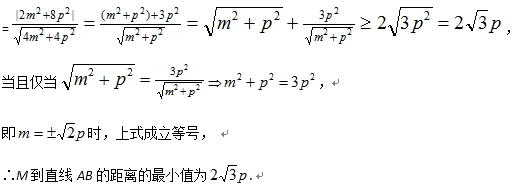- 圆锥曲线与方程
- 共2626题
12.若点P(3,m)在以点F为焦点的抛物线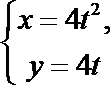
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.已知抛物线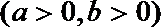

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.设







正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.抛物线y=ax2(a≠0)的焦点坐标是____________.
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.过抛物线



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.已知抛物线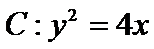
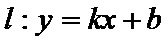
(Ⅰ)当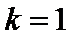
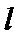
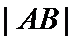
(Ⅱ)当直线OA,OB的倾斜角之和为45°时,求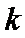
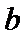
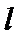
正确答案
(1)抛物线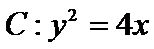
由已知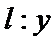
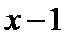
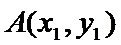
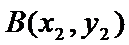
联立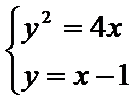
消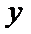
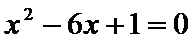
所以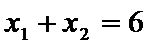
(2)联立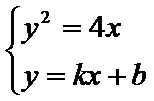
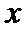
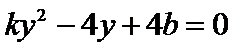
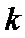
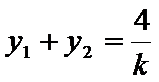
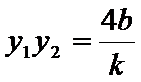
设直线OA,OB的倾斜角分别为α,β,斜率分别为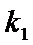
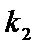
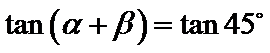
其中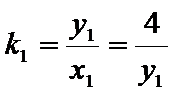
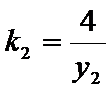
所以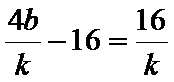
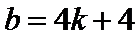
此时,使(*)式有解的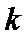
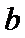
直线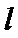
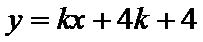
消去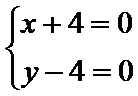
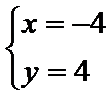
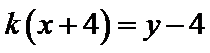
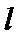
解析
解析已在路上飞奔,马上就到!
知识点
12.已知函数

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
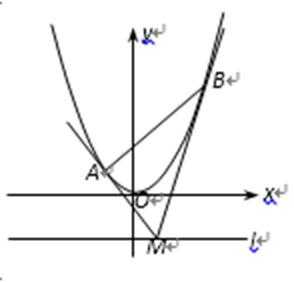
20. 如图,设抛物线方程为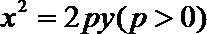
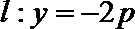
(1)设抛物线上一点P到直线l的距离为d,F为焦点,当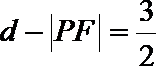
(2)求M到直线AB的距离的最小值。
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.已知点A(3,2),F为抛物线

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.过抛物线y2=2px(p>0)的焦点F作直线l,交抛物线于A、B两点,交其准线于C点,若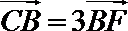
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.设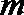
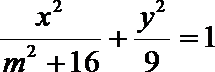

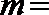
正确答案
3
解析
解析已在路上飞奔,马上就到!
知识点
20.如图,已知抛物线










(1)求抛物线
(2)当


(3)若直线



正确答案
(1)∵点

∴


(2)法一:∵当



设

∴

∴

法二:∵当


∴


∴直线

联立方程组

∵


同理可得


(3)法一:设


可得,直线

同理,直线

∴

∴直线



∵



法二:设点


以


⊙

①-②得:直线

当



∵



解析
解析已在路上飞奔,马上就到!
知识点
16. 设坐标原点为O,抛物线

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.如果点P到点

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.若抛物线


正确答案
4
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析