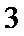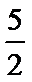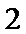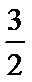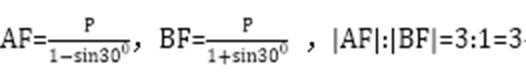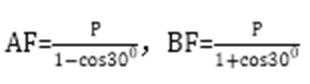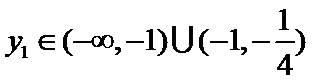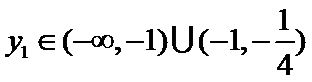- 圆锥曲线与方程
- 共2626题
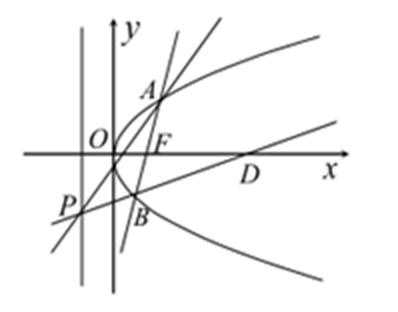
如图(7),已知抛物线C:
23.当直线l的倾斜角是45°时,AB的中垂线交y轴于点Q(0,5),求p的值;
24.以AB为直径的圆交x轴于M,N两点,记劣弧

正确答案
(1)
解析
解:(1)



设







考查方向
解题思路
(1)首先设出直线AB方程,再计算出中点从而确定其中垂线方程,最后将Q点坐标代入方程算出P的值(2)根据题意设出直线L的方程,表示出弦AB和圆心D的坐标;令


易错点
对条件
正确答案
(2)
解析
解:
(2)设




令


当


故

考查方向
解题思路
(1)首先设出直线AB方程,再计算出中点从而确定其中垂线方程,最后将Q点坐标代入方程算出P的值(2)根据题意设出直线L的方程,表示出弦AB和圆心D的坐标;令


易错点
对条件
10.在平面直角坐标系xOy中,抛物线y2=2px(p>0) 的焦点为F,双曲线
正确答案
y=±2x
解析
抛物线y2=2px(p>0)的焦点为F
双曲线

代入抛物线的方程,可得A
由A,B,F三点共线,可得:
考查方向
解题思路
求得抛物线的焦点,双曲线的渐近线方程,代入抛物线的方程可得A,B,再由A,B,
F共线,可得
易错点
混淆抛物线和双曲线的几何性质,同时计算容易出现错误
知识点
10.设直线l与抛物线

正确答案
解析
不妨设直线




代入


可得


考查方向
解题思路
先设直线方程后代人消元得到判别式






易错点
1.不会转化题中给出的条件这样的直线l恰有4条;
找不到r和t之间的关系导致没有思路。
知识点
14.若抛物线C:

正确答案


解析
直线

























考查方向
解题思路
1)根据直线过定点和抛物线的方程判定位置关系;
2)设出与直线
3)利用点到直线的距离进行求解.
易错点
本题易在讨论

知识点
已知抛物线









23.求
24.若圆




正确答案
(1)抛物线

解析
试题分析: 本题属于抛物线、直线、圆的方程及位置关系考查题型,意在考查考生的分析问题、解决问题的能力及运算能力。
(Ⅰ)设

又∵以


∴




考查方向
解题思路
(1)直线








(2)通过直线

易错点
以


正确答案
(2)直线

圆
解析
试题分析: 本题属于抛物线、直线、圆的方程及位置关系考查题型,意在考查考生的分析问题、解决问题的能力及运算能力。
(Ⅱ)设直线


化简整理得
∴


∴圆心

∵圆


∴
∴

此时直线


圆心

圆

考查方向
解题思路
(1)直线








(2)通过直线

易错点
以


13. 抛物线
正确答案
解析

考查方向
解题思路
先化为标准方程,结合图形直接求准线方程。
易错点
没有变为标准方程,直接得出x=2、
知识点
4.已知抛物线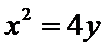
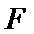
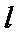
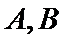
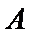
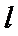
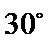
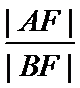
正确答案
解析
考查方向
解题思路
根据题意, 直接用焦半径表示AF与BF的长度.
易错点
忽略直线过焦点,导致AF与BF的长度无法用3
知识点
抛物线C的方程为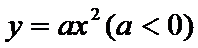
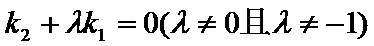
24.求抛物线C的焦点坐标和准线方程;
25.设直线AB上一点M,满足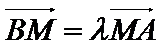
26.当
正确答案
(1)焦点坐标为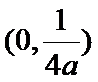
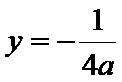
解析
(Ⅰ)由抛物线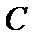
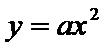
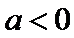
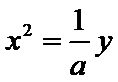
焦点坐标为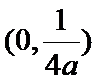
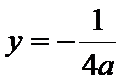
考查方向
解题思路
根据抛物线的几何性质直接得到即可;
易错点
无
正确答案
(2)略;
解析
(Ⅱ)证明:设直线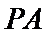
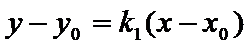
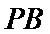
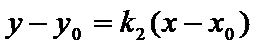
点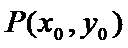
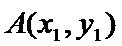
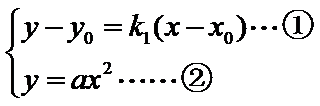
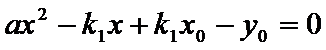
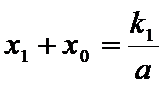
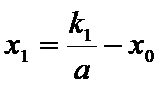
又点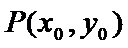
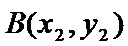
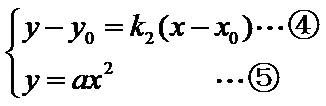
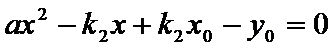
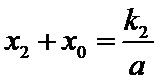
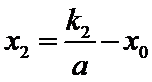
由已知得,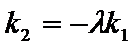
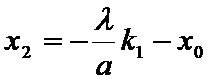
设点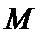
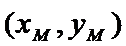
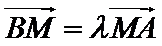
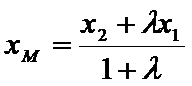
将③式和⑥式代入上式得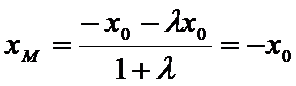
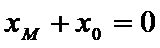
∴线段
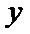
考查方向
解题思路
1
先根据条件求出A,B的横坐标后带入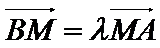
易错点
不会求解点A,B的坐标,运算量大;
正确答案
(3)
解析
(Ⅲ)因为点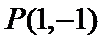
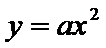
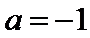
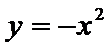
由③式知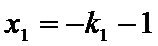
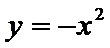
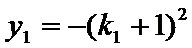
将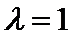
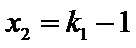
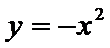
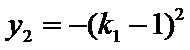
因此,直线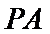
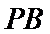
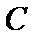
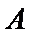
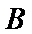
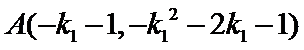
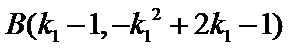
于是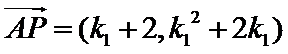
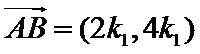
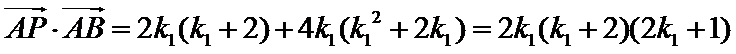
因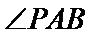
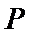
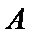
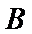
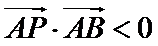
求得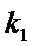
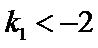
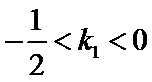
又点
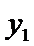
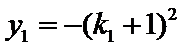
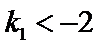
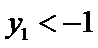
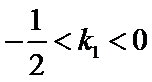
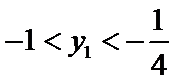
考查方向
解题思路
先求出抛物线的方程,然后根据第(2)问求出点A,B的坐标,然后将∠PAB为钝角转化为向量求解即可。
易错点
不会转化题中给出的条件∠PAB为钝角,导致做不出正确答案。
14.如图,探照灯反射镜的纵截面是抛物线的一部分,光源在抛物线的焦点F处,灯口直径AB为



正确答案


解析
.建立如图平面直角坐标系,设抛物线方程为
则点A(40,30)在抛物线上, 

考查方向
解题思路
1.建立平面直角坐标系设出抛物线的方程;
2.根据题意点A(40,30)在抛物线上求出p;
易错点
不会将题中给出的应用问题建立坐标系求解;
知识点
过抛物线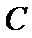

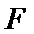
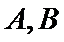

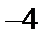
23.求抛物线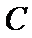
24.已知点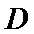

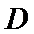
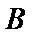
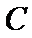
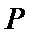
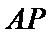
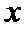
正确答案
详见解析
解析
(1)抛物线的焦点为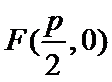
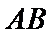
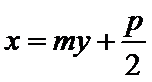
由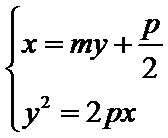
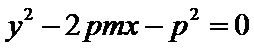
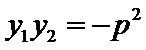
∴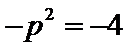

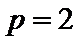
∴抛物线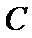
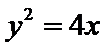
考查方向
抛物线的性质及应用,抛物线的方程
解题思路
设出参数,建立等量关系 列出方程,求解方程 求出参数
易错点
计算能力弱
正确答案
详见解析
解析
(2)依题意,直线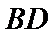

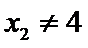
∴直线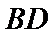

∵抛物线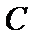
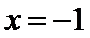
由①,②联立方程组可求得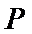
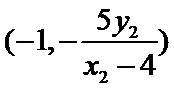
由(1)可得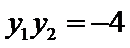
∴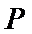
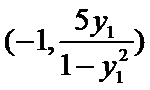
∴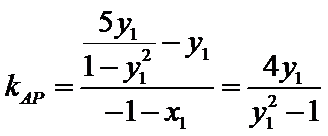
∴直线
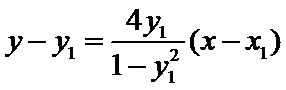
令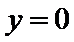
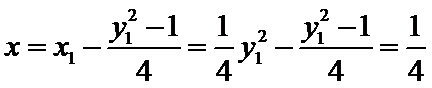
∴直线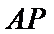
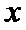
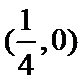
考查方向
直线和抛物线的交汇问题,直线和圆锥曲线的综合应用 圆锥曲线中有关定点、定长的问题。
解题思路
先求出抛物线的准线方程,联立方程可得P点的坐标,用含参数的式子表示出直线的斜率,判断其是否能过定点
易错点
计算能力弱,圆锥曲线相关性质掌握不牢固
教师点评
圆锥曲线这类题对考生的计算能力要求很高
已知抛物线C的标准方程为

23.求抛物线C的标准方程;
24.记
正确答案
详见解析
解析
由题意,

抛物线C的标准方程为
考查方向
求抛物线的标准方程
解题思路
根据已知条件建立方程,进而求出参数值,求出抛物线的方程
易错点
计算能力弱,相关公式记忆不准确
正确答案
详见解析
解析
设







(ⅰ)


又

不论a取何值,t均与m有关, 即
(ⅱ)







考查方向
直线和圆锥曲线的交汇问题,新概念定义的和圆锥曲线结合题
解题思路
根据稳定点的定义,结合已知条件和抛物线的性质。联立方程组,求解参数,得到答案
易错点
计算能力弱,分类讨论思想运用不好
8.已知抛物线







正确答案
解析
由一元二次不等式的解集可知方程有两个相等的实数根
所以
当且仅当
考查方向
一元二次不等式的解法
解题思路
根据一元二次不等式的解集和基本不等式求出M+N的最大值
易错点
不会解不等式,不能想到用基本不等式
知识点
已知抛物线





23.求抛物线
24.与圆






正确答案
设
则点



同理,点



两式结合,说明直线



由已知直线


故所求抛物线的方程为
解析
详见解题过程.
考查方向
本题考查抛物线的标准方程,直线与抛物线的关系.
解题思路
先设出点A,B的坐标,进而写出抛物线的切线方程,进而可以写出直线AB的方程,对照已知条件中直线的斜率即可求出p,进而可以写出抛物线的方程;
易错点
若不能根据直线AB的特征写出AB的方程,则可能导致思路受阻.
教师点评
本题把直线与抛物线相切融入到抛物线方程的求解中,命题形式灵活,具有较好的代表性.
正确答案
直线



所以

与抛物线方程联立,即
化简消






设


由

又点


解析
注意向量运算与坐标之间的互相转化.
考查方向
本题考查直线与圆的位置关系,直线与抛物线的关系.
解题思路
先根据直线与圆的相切求出m与k的关系,再把直线与抛物线联立,利用向量的运算及判别式即可求出结论.
易错点
忽略判别式容易导致错误
教师点评
本题具有一定的综合性,对计算能力有较高要求.
定期存款较股票型基金产品有一定特点,下列说法正确的是( )。
A.流动性高;收益率高
B.流动性高;收益率低
C.流动性低;收益率低
D.流动性低;收益率高
正确答案
C
解析
[解析] 一般说来,定期存款低于股票型基金产品的收益率,流动性也低于股票型基金产品。
2. 已知抛物线



其焦点到准线的距离为
正确答案
解析
因为抛物线焦点在




考查方向
解题思路
先找准抛物线的开口,设出方程即可。
易错点
抛物线的标准方程的正确应用。
知识点
扫码查看完整答案与解析