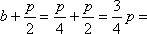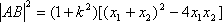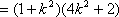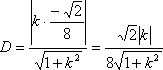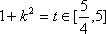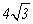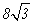- 圆锥曲线与方程
- 共2626题
在直角坐标


(1)在以O为极点,x轴正半轴为极轴的极坐标系中,分别写出圆

(2)求出
正确答案
(1)
(2)
解析
(1)圆C1的极坐标方程为ρ=2,
圆C2的极坐标方程为ρ=4cosθ.
解

故圆C1与圆C2交点的坐标为
注:极坐标系下点的表示不唯一.
(2)(解法一)
由

故圆C1与C2的公共弦的参数方程为
知识点
已知三点O(0,0),A(-2,1),B(2,1),曲线C上任意一点M(x,y)满足
(1)求曲线C的方程;
(2)动点Q(x0,y0)(-2<x0<2)在曲线C上,曲线C在点Q处的切线为l,问:是否存在定点P(0,t)(t<0),使得l与PA,PB都相交,交点分别为D,E,且△QAB与△PDE的面积之比是常数?若存在,求t的值;若不存在,说明理由。
正确答案
见解析
解析
(1)由

得

由已知得
化简得曲线C的方程:x2=4y.
(2)假设存在点P(0,t)(t<0)满足条件,
则直线PA的方程是
曲线C在点Q处的切线l的方程是

由于-2<x0<2,因此-1<
①当-1<t<0时,

②当t≤-1时,

所以l与直线PA,PB一定相交。
分别联立方程组
解得D,E的横坐标分别是

则xE-xD=(1-t)
又|FP|=-


又
于是
=
对任意x0∈(-2,2),要使
解得t=-1.此时
故存在t=-1,使得△QAB与△PDE的面积之比是常数2.
知识点
已知f(x)是定义在R上的偶函数,且以2为周期,则“f(x)为[0,1]上的增函数”是“f(x)为[3,4]上的减函数”的( )
正确答案
解析
由题意,f(x)是定义在R上的偶函数,f(x)为[0,1]上的增函数
所以f(x)为[﹣1,0]上是减函数
又f(x)是定义在R上的函数,且以2为周期[3,4]与[﹣1,0]相差两个周期,故两区间上的单调性一致,所以可以得出f(x)为[3,4]上的减函数,故充分性成立,若f(x)为[3,4]上的减函数,由周期性可得出f(x)为[﹣1,0]上是减函数,再由函数是偶函数可得出f(x)为[0,1]上的增函数,故必要性成立
综上,“f(x)为[0,1]上的增函数”是“f(x)为[3,4]上的减函数”的充要条件。
知识点
过抛物线y2=2x的焦点F作直线交抛物线于A,B两点,若
正确答案
解析
由题意可得:F(
因为过抛物线y2=2x的焦点F作直线l交抛物线于A、B两点,
所以|AF|=

因为
设直线l的方程为y=k(x﹣
联立直线与抛物线的方程可得:k2x2﹣(k2+2)x+
所以x1+x2=
∴
∴k2=24
∴24x2﹣26x+6=0,
∴
∴|AF|=
知识点
在平面直角坐标系xOy中,F是抛物线C:x2=2py(p>0)的焦点,M是抛物线C上位于第一象限内的任意一点,过M,F,O三点的圆的圆心为Q,点Q到抛物线C的准线的距离为
(1)求抛物线C的方程;
(2)是否存在点M,使得直线MQ与抛物线C相切于点M?若存在,求出点M的坐标;若不存在,说明理由;
(3)若点M的横坐标为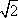


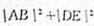
正确答案
见解析。
解析
(1)F抛物线C:x2=2py(p>0)的焦点F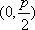
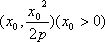
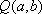
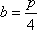

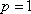

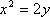
(2)假设存在点M,使得直线MQ与抛物线C相切于点M,
而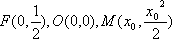
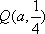
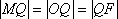
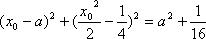
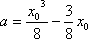
由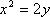
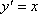
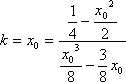
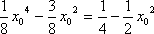
即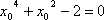
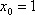
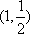
(3)若点M的横坐标为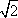
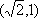
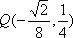
由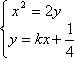
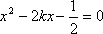
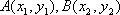
圆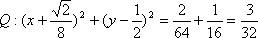
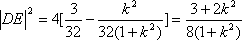
于是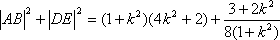
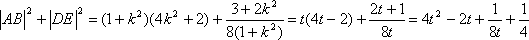
设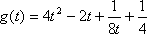
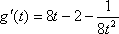
当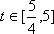
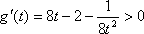
即当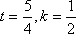
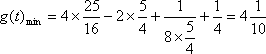
故当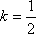
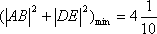
知识点
设抛物线y2=8x的焦点为F,准线为l,P为抛物线上一点,PA⊥l,A为垂足,如果直线AF的斜率为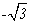
正确答案
解析
抛物线的焦点F(2,0),直线AF的方程为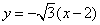
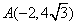
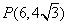
知识点
已知命题
正确答案
解析
命题p为全称命题,所以其否定




知识点
已知定义域为





①对任意









其中所有正确结论的序号是 。
正确答案
①②④
解析
1











知识点
已知等差数列





(1)求数列
(2)令




正确答案
见解析。
解析
(1)
解得
(2)
知识点
已知集合M={1,2,zi},i为虚数单位,N={3,4},M∩N={4},则复数z=( )。
正确答案
解析
由M∩N={4},得zi=4,∴z=
知识点
以下茎叶图记录了甲、乙两组各五名学生在一次英语听力测试中的成绩(单位:分),已知甲组数据的中位数为15,乙组数据的平均数为16.8,则x,y的值分别为( )。
正确答案
解析
由甲组数据中位数为15,可得x=5;而乙组数据的平均数
知识点
已知{an}是等差数列,a1=1,公差d≠0,Sn为其前n项和,若a1,a2,a5成等比数列,则S8=__________.
正确答案
64
解析
由a1=1且a1,a2,a5成等比数列,得a1(a1+4d)=(a1+d)2,解得d=2,故S8=8a1+
知识点
在平面直角坐标系xOy中,将从点M出发沿纵、横方向到达点N的任一路径成为M到N的一条“L路径”。如图6所示的路径

(1)写出点P到居民区A的“L路径”长度最小值的表达式(不要求证明);
(2)若以原点O为圆心,半径为1的圆的内部是保护区,“L路径”不能进入保护区,请确定点P的位置,使其到三个居民区的“L路径”长度之和最小。
正确答案
见解析
解析
设点P的坐标为(x,y).
(1)点P到居民区A的“L路径”长度最小值为



(2)
由题可知,点P到三外居民区的“L路径”长度之和的最小值为点P分别到三个居民区的“L路径”长度最小值之和(记为d)的最小值.
(1) 当
因为 
当且仅当x=3时,不等式(*)中的等号成立。
又因为
当且仅当

类似可得 
(2) 
由(1)知,

故 
综上所述,在点P(3,1)处修建文化中心,可使该文化中心到三个居民区的“L路径”长度之和最小.
知识点
若函数f(x)=x3+ax2+bx+c有极值点x1,x2,且f(x1)=x1,则关于x的方程3(f(x))2+2af(x)+b=0的不同实根个数是( )。
正确答案
解析
解析:
由f′(x)=3x2+2ax+b=0得,x=x1或x=x2,
即3(f(x))2+2af(x)+b=0的根为f(x)=x1或f(x)=x2的解,如图所示,
由图象可知f(x)=x1有2个解,f(x)=x2有1个解,因此3(f(x))2+2af(x)+b=0的不同实根个数为3.
知识点
等轴双曲线






正确答案
解析
设


得:
知识点
扫码查看完整答案与解析