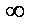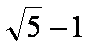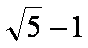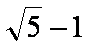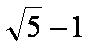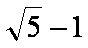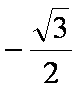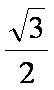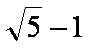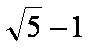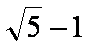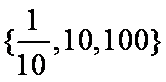- 圆锥曲线与方程
- 共2626题
下列结论中正确的是 。
① 函数y=f(x)是定义在R上的偶函数,且f(x+1)=- f(x),则函数y=f(x)的图像关于直线x=1对称;
②
③
④ 线性相关系数r的绝对值越接近于1,表明两个变量线性相关程度越弱。
正确答案
①②③
解析
略。
知识点
抛物线











正确答案
解析
略
知识点
已知a≥b>0,求证:2a3-b3≥2ab2-a2b.
正确答案
见解析
解析
证明:2a3-b3-(2ab2-a2b)=2a(a2-b2)+b(a2-b2)=(a2-b2)(2a+b)=(a-b)(a+b)(2a+b)。
因为a≥b>0,所以a-b≥0,a+b>0,2a+b>0,
从而(a-b)(a+b)(2a+b)≥0,即2a3-b3≥2ab2-a2b.
知识点
二项式(1+sinx)n的展开式中,末尾两项的系数之和为7,且系数最大的一项的值为

正确答案
解析
略。
知识点
已知椭圆


(1)求椭圆方程;
(2)斜率为







正确答案
(1)椭圆方程为
(2)直线

解析
(1)依题意有



故椭圆方程为
(2)直线

联立方程组


设



则
设



直线


所以
当△

可得

即直线


知识点
已知函数

(1)求



正确答案
(1) 1; (2)
解析
(1)
(2)
因为


所以
所以
知识点
已知实数m>0,定点A(-m,0),B(m,0),s为一动点,直线SA与直线SB的斜率之积
为
(1)求动点s的轨迹C的方程,并指出它是哪一种曲线;
(2)当
正确答案
见解析。
解析
(1)设S(x,y),则
由题意得
当O<m<1时,轨迹C是中心在坐标原点,焦点在y轴上的椭圆(除去椭圆与x轴的两个交点);
当m>l时,轨迹C是中心在坐标原点,焦点在,轴上的椭圆(除去椭圆与x轴的两个交点):
当m=l时,轨迹C是以原点为圆心,半径为l的圆(除去圆与x轴的两个交点)。
(2)当
由
①令
此时直线l与曲线C有且只有一个公共点,
②令△>0且直线2x-y+1=O恰好过点(
此时直线与曲线C有且只有一个公共点,
综上所述,当t=±3或
知识点
已知直线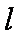
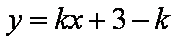
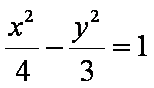
正确答案
解析
略
知识点
已知集合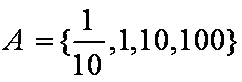
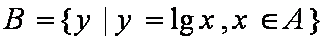
正确答案
解析
因为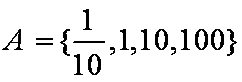
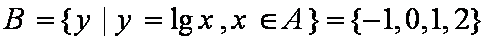
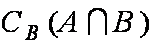
知识点
已知椭圆C:




(1)求椭圆C的方程;
(2)AB是经过右焦点F的任一弦(不经过点P),设直线




正确答案
见解析
解析
(1)由点


由 ①②得


(2)假设存在常数

由题意可设
代入椭圆方程
设

在方程③中,令




即有
所以
=
将④代入⑤得

所以
故存在常数
知识点
12.设






正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.过点



正确答案

解析
解析已在路上飞奔,马上就到!
知识点
21.已知















(1)求轨迹
(2)设点



正确答案
解:
(1)由|PF1|-|PF2|=2<|F1F2|知,点P的轨迹S是以F1、F2为焦点的双曲线右支.
由c=2,2a=2,∴b2=3.故轨迹S的方程为x2-=1 (x≥1)
(2)当直线l的斜率存在时,设直线方程为y=k(x-2),P(x1,y1),Q(x2,y2)
与双曲线方程联立消y得(k2-3)x2-4k2x+4k2+3=0.
∴


=[4x1x2-2(x1+x2)+1]=x1x2-+
=-+=+=+>.
当斜率不存在时,|AP|·|BQ|=,∴λ的最小值为.
此时,|PQ|=6,|MF2|=3,S△PMQ=|MQ|·|PQ|=9.
解析
解析已在路上飞奔,马上就到!
知识点
若三个非零且互不相等的实数a、b、c满足


(1)“好集” P中的元素最大值为________;
(2)“好集” P的个数为________。
正确答案
(1)2012;(2)1006
解析
因为若集合P中元素a、b、c既是调和的,又是等差的,则





知识点
22.已知函数


(1)求
(2)证明:当
(3)证明:若

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析