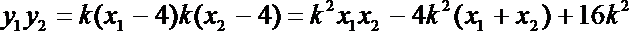- 圆锥曲线与方程
- 共2626题
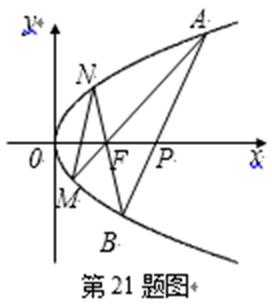
21.如图,已知抛物线






(1)证明


(2)记直线

正确答案
证明:(1)依题意,设直线

将其代入

整理得 
从而
于是
∴

又
(2)证明:设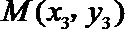
则 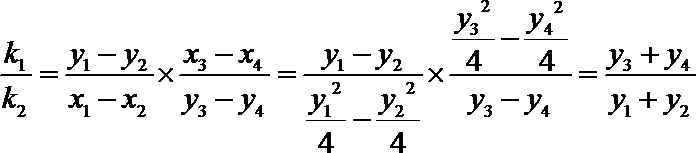
设直线

将其代入

整理得
∴
同理可得 
故
由(1)知,
∴
解析
解析已在路上飞奔,马上就到!
知识点
19.已知椭圆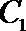
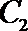

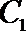

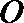
(1)求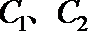
(2)过曲线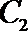
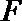
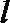
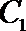
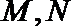
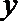
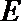
若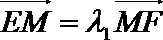
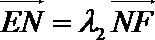
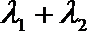
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.已知椭圆C:


(Ⅰ)求椭圆C的标准方程
(Ⅱ)若直线L:
求证:
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.已知点
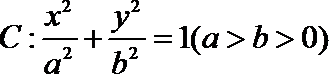
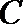
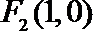
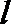
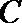
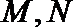
(1)求椭圆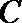
(2)若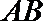
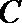
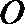
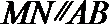
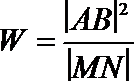
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.已知椭圆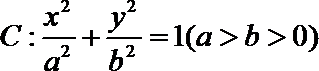

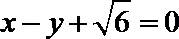
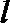
(1)求椭圆C的方程;
(2)求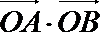
(3)若B点在于x轴的对称点是E,证明:直线AE与x轴相交于定点。
正确答案
(1)解:由题意知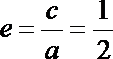
∴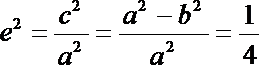
又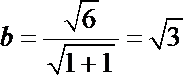
∴
故椭圆的方程为
(2)解:由题意知直线l的斜率存在,设直线l的方程为
由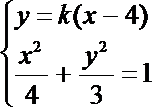
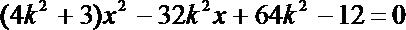
由
得:
设A(x1,y1),B (x2,y2),则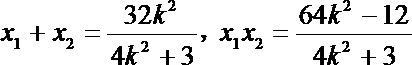
∴
解析
解析已在路上飞奔,马上就到!
知识点
21.已知椭圆C的离心率
(I)求椭圆C的方程;
(II)设直线x=my+1与椭圆C交于P,Q两点,直线A1P与A2Q交于点S,试问:当m变化时,点S是否恒在一条定直线上?若是,请写出这条直线方程,并证明你的结论;若不是,请说明理由.
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.已知椭圆C:
(1)求椭圆C的方程;
(2)过点Q(4,0)且不与坐标轴垂直的直线l交椭圆C于A、B两点,设点A关于x轴的对称点为A1.求证:直线A1B过x轴上一定点,并求出此定点坐标.
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.已知椭圆C:+=1(a>b>0)的离心率e=,椭圆C的上、下顶点分别为A1,A2,左、右顶点分别为B1,B2,左、右焦点分别为F1,F2.原点到直线A2B2的距离为.
(1)求椭圆C的方程;
(2)过原点且斜率为的直线l,与椭圆交于E,F点,试判断∠EF2F是锐角、直角还是钝角,并写出理由;
(3)P是椭圆上异于A1,A2的任一点,直线PA1,PA2,分别交
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
22.设






(1)对任意





(2)若点


(3)对(1)中点







正确答案
(1)直线






(2)若点


(方法1)两边同除以

∴点

(方法2) 设

得
即


(3)(方法1)设

由
① 当直线
设


②当直线
设



即原点到直线


∴直线

(方法2)设

则
即
注意到圆

∴
即原点到直线

∴直线

解析
解析已在路上飞奔,马上就到!
知识点
5.过点M(-2,0)的直线l与椭圆x2+2y2=2交于P1,P2,线段P1P2的中点为P。设直线l的斜率为k1(k1≠0),直线OP(O为坐标原点)的斜率为k2,则k1k2等于( )
正确答案
解析
设P1(x1,y1),P2(x2,y2),P(x0,y0),则






知识点
18. 平面直角坐标系






(1)求椭圆
(2)过椭圆




①设直线




②若连接





正确答案
见解析
解析
(1)由题意知



所以椭圆C的标准方程为
(2)①M
②点


∵

∴


∵点P在椭圆C上, ∴
∴


∵
∴
∴

考查方向
解题思路
本题考查导数的性质,解题步骤如下:
(1)根据离心率和几何特点,求出椭圆方程
(2)表示M,N进而得
(3)表示

易错点
点M,N表示不当
知识点
20.已知抛物线





(1)若线段


(2) 若



正确答案
(1)
(2)
解析
本题属于圆锥曲线的基本问题,题目的难度是逐渐由易到难,
(1)由直线的参数表示出点
(2)根据弦长公式求出

(1)法一:
设



(1)当


(2)当

综上:
(1)法二:

设




(2)

考查方向
本题考查了求轨迹方程的方法、中点弦的处理方法、弦长公式及面积问题,常见求轨迹方程的方法有直译法、定义法、相关点法及参数法。圆锥曲线常见的问题有弦长、中点、面积、角度和“定”问题——定点、定线和定值。
易错点
1、求轨迹方程方法不熟练和点差法如何处理中点弦。
2、含参运算不正确导致出错。
知识点
22.如图,
曲线




当

(1)若猫眼曲线




(2)对于题(1)中的求猫眼曲线







(3)若斜率为









正确答案
(1)

(2)略;
(3)
解析
(1)



(2)设斜率为


线段


得



且
即
同理,
(3)设直线


化简得


联立方程
化简得


两平行线间距离:



注:若用第一小题结论,
算得:


考查方向
本题主要考查椭圆的标准方程与性质,考查椭圆与直线的位置关系,考查化简运算能力与对新定力的概念的即时学习能力.
解题思路
(1)根据定义求得猫眼曲线Γ的方程;
(2)设交点







(3)设直线



易错点
1.对新定义的“猫眼曲线”的概念的不理解,即时学习能力不够;
2.解析几何中繁琐的化简容易出错,特别是带字母的化简运算.
知识点
19.已知椭圆



(Ⅰ)求椭圆
(Ⅱ)设动直线










正确答案
(Ⅰ)椭圆
解析
(Ⅰ)解:由题意,得

又因为点

所以
解得


所以椭圆C的方程为
(Ⅱ)证明:当直线


易得直线


当直线


由方程组

因为直线
所以

由方程组

设



所以

将
得
综上,

考查方向
解题思路
1、每一问通过椭圆离心率,点


2、第二问求证






易错点
对于第二问不考虑斜率存在与否直接解答从而导致考虑不全面而失分。
知识点
正确答案
知识点
扫码查看完整答案与解析