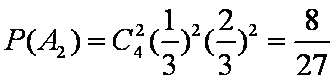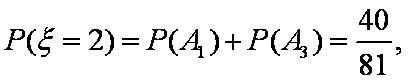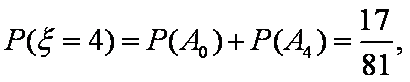幂函数的概念、解析式、定义域、值域
共1030题

· 幂函数的概念、解析式、定义域、值域

幂函数的概念、解析式、定义域、值域
共1030题

热门试卷

X 查看更多试卷

题型：简答题

简答题 · 12 分

设函数，函数分别在和处取得极值，且。

（1）求的值。

（2）求证：在区间上是增函数；

（3）设在区间上的最大值和最小值分别为和，试问当实数为何值时，取得最小值？并求出最小值。

正确答案

见解析

解析

（1）解：的两根为

（2）解：

，在区间上为增函数

（3）解：由（2）可知，，，

时取等号，

必有

又

整理可得

又可验证此时

知识点

幂函数的概念、解析式、定义域、值域

题型：简答题

简答题 · 12 分

已知各项都不相等的等差数列的前项和为，且为和的等比中项。

（1）求数列的通项公式；

（2）若数列满足，且，求数列的前项和。

正确答案

见解析。

解析

（1）设等差数列的公差为()，

则解得 ∴。

（2）由， ∴，

。

∴，

∴

知识点

幂函数的概念、解析式、定义域、值域

题型：填空题

填空题 · 5 分

已知函数，则满足不等式f（1﹣x2）＞f（2x）的x的范围是　　。

正确答案

解析

由题意，可得

故答案为：

知识点

幂函数的概念、解析式、定义域、值域

题型：简答题

简答题 · 12 分

设A,B是椭圆上的两点，为坐标原点。

（1）设，, .求证:点M在椭圆上;

（2）若,求的最小值.

正确答案

见解析。

解析

（1）设,则

则

故点M在椭圆上。

（2）设,,,

则

从而故

知识点

幂函数的概念、解析式、定义域、值域

题型：简答题

简答题 · 12 分

现有4个人去参加春节联欢活动，该活动有甲、乙两个项目可供参加者选择. 为增加趣味性，约定：每个人通过掷一枚质地均匀的骰子决定自己去参加哪个项目联欢，掷出点数为1或2的人去参加甲项目联欢，掷出点数大于2的人去参加乙项目联欢。

（1）求这4人中恰好有2人去参加甲项目联欢的概率；

（2）求这4个人中去参加甲项目联欢的人数大于去参加乙项目联欢的人数的概率；

（3）用X，Y分别表示这4个人中去参加甲、乙项目联欢的人数，记，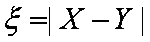

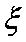
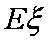
求随机变量的分布列与数学期望.

正确答案

见解析。

解析

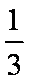
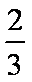
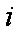
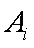
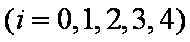
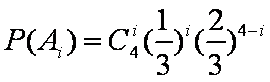
依题意，这4个人中，每个人去参加甲项目联欢的概率为，去参加乙项目联欢的概率为.设“这4个人中恰有人去参加甲项目联欢”为事件，，则.

（1）这4个人中恰好有2人去参加甲项目联欢的概率

（2）设“这4人中去参加甲项目联欢的人数大于去参加乙项目联欢的人数”为事件，，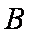

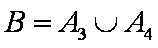
故.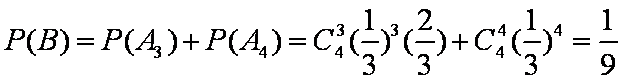

∴这4人中去参加甲项目联欢的人数大于去参加乙项目联欢的人数的概率为.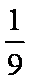

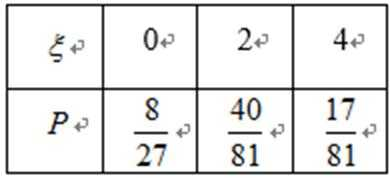
（3）的所有可能取值为0,2,4.

，

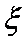
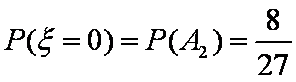
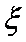
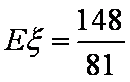
所以的分布列是

知识点

幂函数的概念、解析式、定义域、值域

继续学习学习下一知识点

下一知识点 : 幂函数的图像

百度题库 > 高考 > 理科数学 > 幂函数的概念、解析式、定义域、值域

扫码查看完整答案与解析