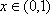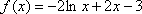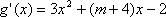- 幂函数的概念、解析式、定义域、值域
- 共1030题
已知函数




(1)已知


(2)若存在


(3)设函数










正确答案
见解析。
解析
(1)





(2)


由

由于



从而

设




从而


所以

(3)设











由于

当


当

令








综上可知,

知识点
已知锐角








(1)求角
(2)设函数



正确答案
(1)
(2)
解析
(1)因为
所以


所以

(2)
由已知
因为



所以

知识点
已知椭圆





(1)求该椭圆的标准方程;
(2)当点













正确答案
见解析
解析
(1)由











故椭圆的标准方程为
(2)设

则






由
设




因为点

所以
故
所以







知识点
已知函数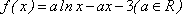
(1)若a=-1,求函数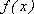
(2)若函数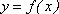

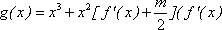
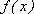
(3)求证: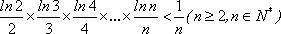
正确答案
见解析
解析
(1)当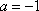
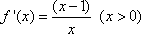
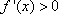
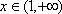
解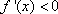
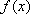


(2) ∵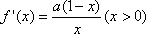
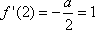
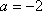
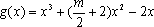
∵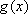
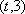
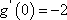
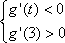
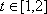
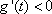
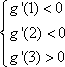
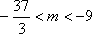
(3)证明如下: 由(1)可知当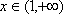
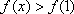
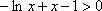
∴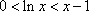
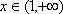
∵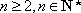
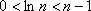
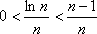
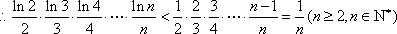
知识点
设集合
正确答案
解析
略
知识点
扫码查看完整答案与解析