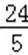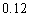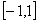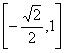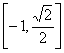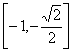- 幂函数的概念、解析式、定义域、值域
- 共1030题
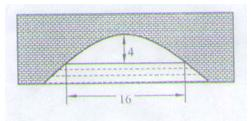
如图,抛物线形拱桥的顶点距水面4米时,测得拱桥内水面宽为16米;当水面升高3米后,拱桥内水面的宽度为 _________米。 、
正确答案
8
解析
略
知识点
在四棱锥






(1)求证:

(2)求证:

(3)设





正确答案
见解析。
解析
(1)取




∴





∴



∴
(2)平面




在直角梯形ABCD中,
∴

又由


又


(3)如图,以D为原点建立空间直角坐标系

平面






∴

知识点
设

正确答案
解析


知识点
如图所示,AB是⊙O的直径,过圆上一点E作切线ED⊥AF,交AF的延长线于点D,交AB的延长线于点C,若CB=2,CE=4,则⊙O 的半径长为 ;AD的长为 。
正确答案
3;
解析
设r是⊙O的半径,由切割线定理可知:CE2=CA•CB,
即42=(2r+2)×2,解得r=3。
因为EC是圆的切线,所以OE⊥EC,AD⊥DC,
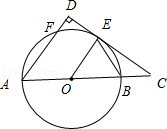
所以△ADC∽△OEC,所以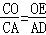
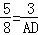
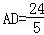
故答案为:3;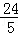
知识点
如图1,



















(1)求
(2)试写出三角形观光平台


正确答案
(1)
解析
(1)由题意,得


又因为过点M要分别修建与OA、OB平行的栈桥MG、MK,
所以

所以

(2)由题意,得
所以
则
因为函数

所以当
知识点
已知函数


正确答案
解析
略
知识点
把容量是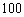
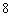
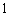
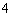
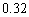
正确答案
解析
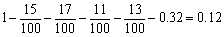
知识点
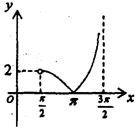
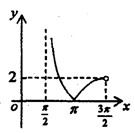
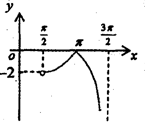
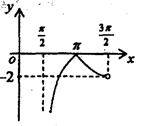
函数y=tanx+sinx-|tanx-sinx|在区间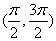
正确答案
解析
略
知识点
已知函数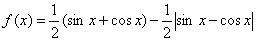
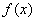
正确答案
解析
略
知识点
已知





正确答案
解析
略
知识点
扫码查看完整答案与解析