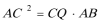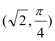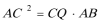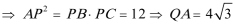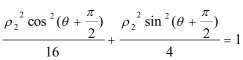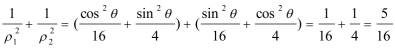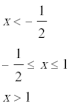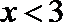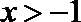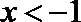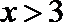幂函数的概念、解析式、定义域、值域
共1030题

· 幂函数的概念、解析式、定义域、值域

幂函数的概念、解析式、定义域、值域
共1030题

热门试卷

X 查看更多试卷

题型：简答题

简答题 · 10 分

请考生在第22、23、24三题中任选一题作答，如果多做，则按所做的第一题记分.

22．选修4—1：几何证明选讲

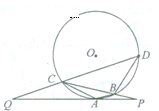
已知PQ与圆O相切于点A，直线PBC交圆于B、C两点，D是圆上一点，且AB∥CD，DC的延长线交PQ于点Q

（1）求证：

（2）若AQ=2AP，AB=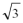,BP=2，求QD.

23．选修4—4：坐标系与参数方程

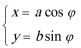
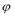
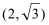
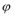
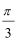
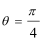
在平面直角坐标系中，曲线C1的参数方程为（a＞b＞0，为参数），以Ο为极点，x轴的正半轴为极轴建立极坐标系，曲线C2是圆心在极轴上且经过极点的圆，已知曲线C1上的点M 对应的参数= ，与曲线C2交于点D

（1）求曲线C1，C2的方程；

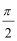
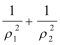
（2）A（ρ1，θ），Β（ρ2，θ+）是曲线C1上的两点，求的值。

24．选修4—5：不等式选讲

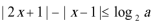
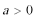
已知关于x的不等式（其中）．

（1）当时，求不等式的解集；

（2）若不等式有解，求实数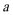的取值范围

正确答案

22.（1）因为AB∥CD，所以∠PAB=∠AQC,

又PQ与圆O相切于点A，所以∠PAB=∠ACB,

因为AQ为切线，所以∠QAC=∠CBA,

所以△ACB∽△CQA,所以,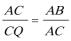

所以

（2）因为AB∥CD，AQ=2AP，

所以,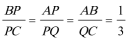

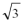
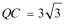
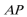
由AB=,BP=2得,PC=6

为圆O的切线

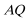
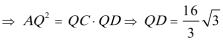
又因为为圆O的切线

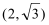
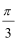
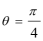
23.解：（1）将M及对应的参数φ= ，；

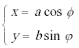
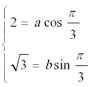
代入得，

所以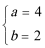，所以C1的方程为，

设圆C2的半径R，则圆C2的方程为：ρ=2Rcosθ（或（x-R）2+y2=R2），

∴R=1 ∴圆C2的方程为：ρ=2cosθ（或（x-1）2+y2=1）

（2）曲线C1的极坐标方程为：，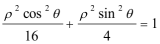

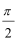
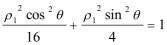
将A（ρ1，θ），Β（ρ2，θ+）代入得：，

所以

即的值为。

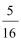
24.解：（1）当a=4时，不等式即|2x+1|-|x-1|≤2，

当x＜−时，不等式为-x-2≤2，解得−4≤x＜−；

当−≤x≤1时，不等式为 3x≤2，解得−≤x≤ ；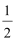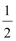

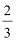
当x＞1时，不等式为x+2≤2，此时x不存在．

综上，不等式的解集为{x|−4≤x≤}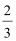

（2）设f（x）=|2x+1|-|x-1|=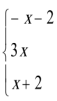

故f（x）的最小值为−，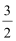

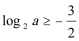
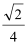
所以，当f（x）≤log2a有解，则有，解得a≥，

即a的取值范围是。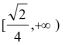

解析

解析已在路上飞奔，马上就到！

知识点

幂函数的概念、解析式、定义域、值域

题型：单选题

单选题 · 3 分

14．有四个幂函数：①； ②； ③； ④．某同学研究了其中的一个函数，他给出这个函数的两个性质：

（1）定义域是{x| xR，且x≠0}；（2）值域是{y| yR，且y≠0}．

如果这个同学给出的两个性质都是正确的，那么他研究的函数是（）

A①

B②

C③

D④

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

幂函数的概念、解析式、定义域、值域

题型：单选题

单选题 · 5 分

2.设为等比数列的前项和，,则（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

幂函数的概念、解析式、定义域、值域

题型：单选题

单选题 · 5 分

10.在等差数列中，表示其前n项和，若，则的符号是（）

A正

B负

C非负

D非正

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

幂函数的概念、解析式、定义域、值域

题型：单选题

单选题 · 5 分

9．若等差数列满足，则的最大值为（）

A60

B50

C45

D40

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

幂函数的概念、解析式、定义域、值域

题型：填空题

填空题 · 4 分

15．已知是关于x的方程的两个根，则=（）．

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

幂函数的概念、解析式、定义域、值域

题型：简答题

简答题 · 14 分

18．在中，角，，的对边分别为，，，已知.

（1）求；

（2）若，求的取值范围。

正确答案

（1）由正弦定理知：

代入上式

得：

即

（2）由（1）得：

其中，

解析

解析已在路上飞奔，马上就到！

知识点

幂函数的概念、解析式、定义域、值域

题型：单选题

单选题 · 3 分

2．不等式的解集是（）

C或

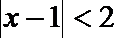
正确答案

解析

解析已在路上飞奔，马上就到！

知识点

幂函数的概念、解析式、定义域、值域

题型：单选题

单选题 · 3 分

13．如图，D是△ABC的边AB的三等分点，则向量等于（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

幂函数的概念、解析式、定义域、值域

题型：简答题

简答题 · 15 分

20．已知数列的首项为，前项和为，且有，．

（1）求数列的通项公式；

（2）当,时，若对任意，都有，求k的取值范围；

（3）当时，若，求能够使数列为等比数列的所有数对。

正确答案

（1）当时，由解得

当时，，

，即

又，综上有，

即是首项为，公比为t的等比数列

（2），所以.

（3），

由题设知为等比数列，所以有

，解得，即满足条件的数对是．

（或通过的前3项成等比数列先求出数对，再进行证明）

解析

解析已在路上飞奔，马上就到！

知识点

幂函数的概念、解析式、定义域、值域

继续学习学习下一知识点

下一知识点 : 幂函数的图像

百度题库 > 高考 > 理科数学 > 幂函数的概念、解析式、定义域、值域

扫码查看完整答案与解析