- 直线的倾斜角与斜率
- 共186题
1
题型:简答题
|
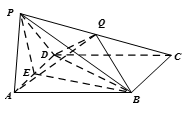
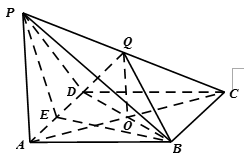
如图,四棱锥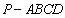
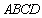
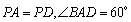
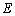
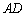
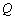
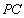
(1)求证: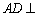
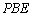
(2)若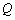
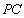
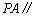
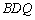
(3)若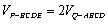
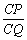
正确答案
见解析
解析
(1)证明:因为 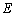
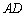
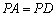
所以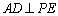
因为底面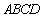
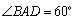
所以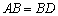
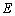
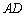
所以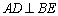
因为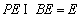
所以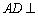
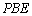
(2)证明:连接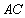
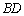
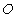
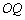
因为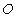
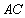
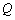
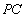
所以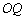
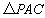
所以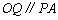
因为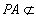
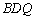
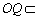
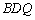
所以
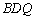
(3)解:设四棱锥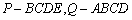
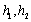
所以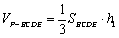
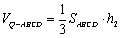
因为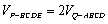

所以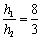
因为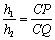
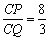
知识点
直线的倾斜角与斜率
1
题型:
单选题
|
已知直线




正确答案
A
解析
略
知识点
直线的倾斜角与斜率
1
题型:填空题
|
如图4,过点P的直线与圆O相交于A,B两点,若PA=1,AB=2,PO=3,则圆O的半径等于_____________________.
正确答案
解析
知识点
直线的倾斜角与斜率
1
题型:
单选题
|
过点

正确答案
A
解析
知识点
直线的倾斜角与斜率
1
题型:简答题
|
如图,三棱柱









(1)求证:

(2)在棱


1

正确答案
见解析。
解析
(1)证明:
取


又

在三棱柱








(2)设

部分的体积之比为1︰15,
则


所以符合要求的点
知识点
直线的倾斜角与斜率
下一知识点 : 三点共线问题
扫码查看完整答案与解析