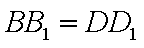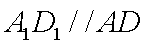- 直线的倾斜角与斜率
- 共186题
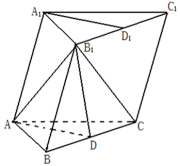
在如图的多面体中,









(1)求证:

(2)求证:
(3)求多面体
正确答案
见解析。
解析
(1)证明:∵

又∵



∴四边形

∵





(2)证明:∵




又




过





∵


∵


∴



又





∵


(3)∵




由(2)知四边形

∴
知识点
如图1,





(1)证明:
(2)设







正确答案
见解析
解析
(1)∵











(2)连接





∵














知识点
已知直线ax+by﹣1=0(a,b不全为0)与圆x2+y2=50有公共点,且公共点的横、纵坐标均为整数,那么这样的直线有( )
正确答案
解析
解:当x≥0,y≥0时,圆上横、纵坐标均为整数的点有(1,7)、(5,5)、(7,1),
根据题意画出图形,如图所示:
根据圆的对称性得到圆上共有3×4=12个点横纵坐标均为整数,
经过其中任意两点的割线有C122=66条,过每一点的切线共有12条,
上述直线中经过原点的有6条,如图所示,
则满足题意的直线共有66+12﹣6=72条。
知识点
如图,在棱长均为4的三棱柱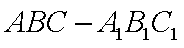
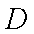
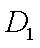
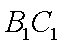
(1)求证: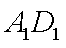
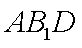
(2)若平面ABC⊥平面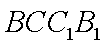
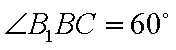
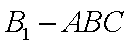
正确答案
见解析
解析
(1)证明:
如图,连结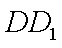
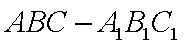
因为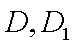

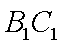
所以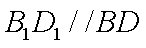

所以四边形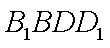
所以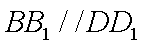
又因为
所以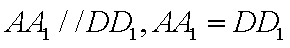
所以四边形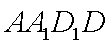
又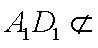
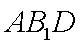
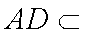
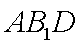

(2)在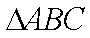
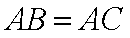
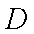

因为平面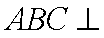
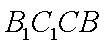

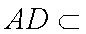
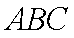
所以
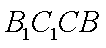
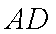
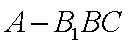
在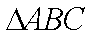
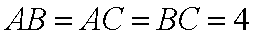
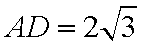
在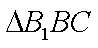
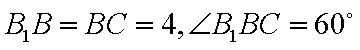
所以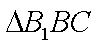
所以三棱锥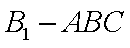
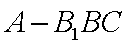
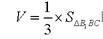
知识点
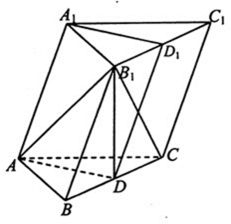
如图,棱柱ABCD—A1B1C1D1的所有棱长都等于2,∠ABC=60°,平面AA1C1C⊥平面ABCD,∠A1AC=60°。
(1)证明:BD⊥AA1;
(2)在直线CC1上是否存在点P,使BP//平面DA1C1?若存在,求出点P的位置;若不存在,说明理由。
正确答案
见解析。
解析
(1)在A1作A1O⊥AC于点O,由于平面AA1C1C⊥平面ABCD,由面面垂直的性质定理知,A1O⊥平面ABCD,
又底面为菱形,所以AC⊥BD
(2)
存在这样的点P,连接B1C,因为A1B1

∴四边形A1B1CD为平行四边形。∴A1D//B1C
在C1C的延长线上取点P,使C1C=CP,连接BP
因B1B
∴BB1
则BP//B1C ∴BP//A1D ∴BP//平面DA1C1
知识点
扫码查看完整答案与解析